【题目】如图,∠AOB=90°.∠BOC=30°,OM平分∠AOC,ON平分∠BOC.

(1)求∠MON的度数;
(2)若∠BOC=60°,其他条件不变,则∠MON= ;
(3)若∠AOB=α,其他条件不变,求∠MON的度数;
(4)从上面的结果能看出什么规律?
参考答案:
【答案】(1)45°;(2)45°;(3)![]() ;(4)∠MON的度数始终是∠AOB的一半,与∠BOC的大小没有关系
;(4)∠MON的度数始终是∠AOB的一半,与∠BOC的大小没有关系
【解析】
(1)根据角的平分线定义和角的和差即可求解;
(2)理由同(1);
(3)理由同(1)把∠AOB换成字母表示即可求解;
(4)根据(1)、(2)、(3)的结论即可发现规律.
解:(1)根据题意,得
∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=120°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=![]() ∠AOC=60°,∠CON=
∠AOC=60°,∠CON=![]() BOC=15°,
BOC=15°,
∴∠MON=∠MOC﹣∠CON=60°﹣15°=45°.
答:∠MON的度数为45°.
(2)∠MON=![]() (150﹣60)=45°.
(150﹣60)=45°.
故答案为45°.
(3)∵![]()
∴![]()
∵OM平分∠AOC,ON平分∠BOC,
∴![]() ,∠CON=
,∠CON=![]() BOC=15°,
BOC=15°,
∴![]()
答:∠MON的度数为![]() .
.
(4)∠MON的度数始终是∠AOB的一半,与∠BOC的大小没有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
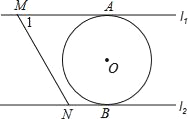
A. MN=
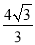 B. 若MN与⊙O相切,则AM=
B. 若MN与⊙O相切,则AM=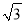
C. l1和l2的距离为2 D. 若∠MON=90°,则MN与⊙O相切
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20
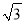 m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45°,求AF的长度.
m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45°,求AF的长度.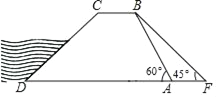
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AC和BC在同一直线上,AC=8cm,BC=3cm,则线段AC的中点和BC中点之间的距离是( )
A.5.5cmB.2.5cm
C.4cmD.5.5cm或2.5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③代数式|x+1|+|x﹣2|取最小值时,相应的整数x的取值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
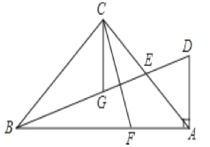
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
-
科目: 来源: 题型:
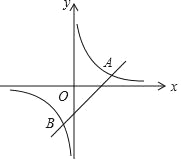
查看答案和解析>>【题目】如图,已知一次函数y=x﹣2与反比例函数y=
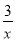 的图象交于A、B两点.
的图象交于A、B两点.(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
相关试题

