【题目】如图所示,将矩形ABCD沿直线AE折叠,顶点D正好落在BC边上F点处,已知CE=3cm, AB=8cm,则图中AD长为______________________.

参考答案:
【答案】10 cm
【解析】
根据折叠以及矩形的对边相等可得:AF=AD=BC,DE=EF.然后根据勾股定理求得CF的长,再设AD=x cm,即可表示BF的长,根据勾股定理进行求解即可.
解:∵矩形ABCD沿直线AE折叠,
∴△ADE和△AFE关于AE成轴对称,AB=CD,AD=BC,
∴AF=AD=BC,EF=DE=DC-CE=8 cm -3 cm =5 cm.
∴CF=![]() =4 cm,
=4 cm,
设AD=xcm,则AF=AD=BC=x cm,BF=(x-4) cm.
在Rt△ABF中,由勾股定理,得x2-82 =(x-4)2.
解得x=10,即AD=10 cm.
故答案为:10 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=
 S△BCD,求点P的坐标.
S△BCD,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】魔术师把四张扑克牌放在桌子上,如图所示,然后蒙住眼睛,请一位观众上台把其中的一张处牌旋转180°放好,魔术师解开蒙着的眼睛的布后,看到四张牌如图23-2-8所示,他很快确定了被旋转的那一张牌,聪明的同学们,你知道哪一张牌被观众旋转过吗?说说你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,若AC=2,则四边形OCED的周长为( )

A.16B.8C.4D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;
(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB,BC,
 .
. 求作:矩形ABCD.

老师说甲、乙同学的作图都正确. 请你选择其中一位同学的作业说明其作图依据.
我选择____同学,他的作图依据是:___________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
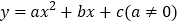 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:①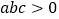 ;②
;②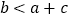 ;③
;③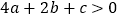 ;④
;④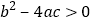 ,其中正确的结论的序号是( )
,其中正确的结论的序号是( )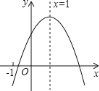
A. ①② B. ①③ C. ③④ D. ②④
相关试题

