【题目】如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;
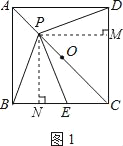
(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;
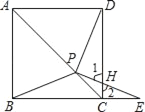
(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.

参考答案:
【答案】(1)PE与PD的数量关系和位置关系分别为:PE=PD,PE⊥PD;(2)成立,理由见解析;(3)成立,理由见解析.
【解析】
(1)根据点P在线段AO上时,利用三角形的全等判定可以得出PE⊥PD,PE=PD;
(2)利用三角形全等得出,BP=PD,由PB=PE,得出PE=PD,要证PE⊥PD;从三方面分析,当点E在线段BC上(E与B、C不重合)时,当点E与点C重合时,点P恰好在AC中点处,当点E在BC的延长线上时,分别分析即可得出;
(3)利用PE=PB得出P点在BE的垂直平分线上,利用垂直平分线的性质只要以P为圆心,PB为半径画弧即可得出E点位置,利用(2)中证明思路即可得出答案.
(1)当点P在线段AO上时,
在△ABP和△ADP中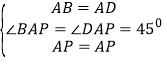 ,
,
∴△ABP≌△ADP,
∴BP=DP,
∵PB=PE,
∴PE=PD,
过点P做PM⊥CD于点M,作PN⊥BC,于点N,
∵PB=PE,PN⊥BE,
∴BN=NE,
∵BN=DM,
∴DM=NE,
在Rt△PNE与Rt△PMD中,
∵PD=PE,NE=DM,
∴Rt△PNE≌Rt△PMD,
∴∠DPM=∠EPN,
∵∠MPN=90°,
∴∠DPE=90°,
故PE⊥PD,
PE与PD的数量关系和位置关系分别为:PE=PD,PE⊥PD;
(2)∵四边形ABCD是正方形,AC为对角线,
∴BA=DA,∠BAP=∠DAP=45°,
∵PA=PA,
∴△BAP≌△DAP(SAS),
∴PB=PD,
又∵PB=PE,
∴PE=PD.
(i)当点E与点C重合时,点P恰好在AC中点处,此时,PE⊥PD.
(ii)当点E在BC的延长线上时,如图.
∵△ADP≌△ABP,
∴∠ABP=∠ADP,
∴∠CDP=∠CBP,
∵BP=PE,
∴∠CBP=∠PEC,
∴∠PEC=∠PDC,
∵∠1=∠2,
∴∠DPE=∠DCE=90°,
∴PE⊥PD.
综合(i)(ii),PE⊥PD;
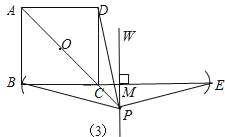
(3)同理即可得出:PE⊥PD,PD=PE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】魔术师把四张扑克牌放在桌子上,如图所示,然后蒙住眼睛,请一位观众上台把其中的一张处牌旋转180°放好,魔术师解开蒙着的眼睛的布后,看到四张牌如图23-2-8所示,他很快确定了被旋转的那一张牌,聪明的同学们,你知道哪一张牌被观众旋转过吗?说说你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,若AC=2,则四边形OCED的周长为( )

A.16B.8C.4D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将矩形ABCD沿直线AE折叠,顶点D正好落在BC边上F点处,已知CE=3cm, AB=8cm,则图中AD长为______________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB,BC,
 .
. 求作:矩形ABCD.

老师说甲、乙同学的作图都正确. 请你选择其中一位同学的作业说明其作图依据.
我选择____同学,他的作图依据是:___________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
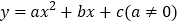 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:①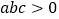 ;②
;②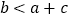 ;③
;③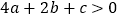 ;④
;④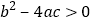 ,其中正确的结论的序号是( )
,其中正确的结论的序号是( )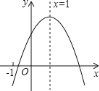
A. ①② B. ①③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,你选择的条件是___(只填写序号).

证明:
相关试题

