【题目】如图,在平面直角坐标系xOy中,直线y=2x+4与y轴交于A点,与x轴交于B点,抛物线C1:y=﹣ ![]() x2+bx+c过A、B两点,与x轴另一交点为C.
x2+bx+c过A、B两点,与x轴另一交点为C. 
(1)求抛物线解析式及C点坐标.
(2)向右平移抛物线C1 , 使平移后的抛物线C2恰好经过△ABC的外心,抛物线C1、C2相交于点D,求四边形AOCD的面积.
(3)已知抛物线C2的顶点为M,设P为抛物线C1对称轴上一点,Q为抛物线C1上一点,是否存在以点M、Q、P、B为顶点的四边形为平行四边形?若存在,直接写出P点坐标;不存在,请说明理由.
参考答案:
【答案】
(1)解:∵直线y=2x+4与y轴交于A点,与x轴交于B点,
∴令x=0,可得y=4,则点A的坐标为A(0,4),
令y=0,可得x=﹣2,则点B的坐标为(﹣2,0),
将A(0,4),B(﹣2,0)代入y=﹣ ![]() x2+bx+c,
x2+bx+c,
可得 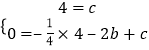 ,
,
解得 ![]() ,
,
∴抛物线C1的解析式为:y=﹣ ![]() x2+
x2+ ![]() x+4,
x+4,
令y=0,则﹣ ![]() x2+
x2+ ![]() x+4=0,
x+4=0,
解得x=8,
∴C点坐标为C(8,0);
(2)解:如图1,
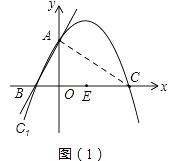
连接AC,
由(1)知,C(8,0),A(0,4),B(﹣2,0),
∴AC2=AO2+OC2=80,AB2=AO2+OB2=20,BC2=102=100,
∴BC2=AC2+AB2,
∴△ABC是直角三角形.
设△ABC的斜边BC的中点为E,则CE= ![]() ×(8+2)=5,
×(8+2)=5,
∴OE=CO﹣CE=3
∴△ABC的斜边BC的中点E的坐标为(3,0),
∵抛物线C2恰好经过△ABC的外心,E为△ABC的外心,
∴OF=3+10=13,即F(13,0),
由E(3,0),F(13,0),得抛物线C2:y=﹣ ![]() (x﹣3)(x﹣13)=﹣
(x﹣3)(x﹣13)=﹣ ![]() x2+4x﹣
x2+4x﹣ ![]() ,
,
联立方程组 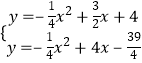 ,
,
解得 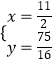 ,即D(
,即D( ![]() ,
, ![]() ),
),
如图2,
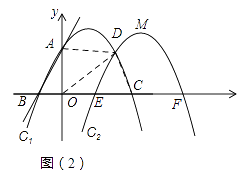
连接AD,OD,CD,则
S四边形AOCD=S△AOD+S△OCD= ![]() ×4×
×4× ![]() +
+ ![]() ×8×
×8× ![]() =
= ![]() ,
,
∴四边形AOCD的面积为 ![]() ;
;
(3)解:存在.点P的坐标为(3,0)或(3,﹣ ![]() )或(3,﹣25).
)或(3,﹣25).
分3种情况:
①如图,当四边形BPMQ为平行四边形时,BP∥QM,BP=QM,
∵抛物线C1中,Q(3, ![]() ),抛物线C2中,M(8,
),抛物线C2中,M(8, ![]() )
)
∴由平移方向可得QM∥x轴,QM=5=BE,
∴BP与x轴重合,
∴点P与点E重合,即P(3,0);
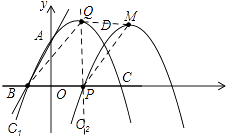
②如图,当四边形BQPM为平行四边形时,PQ∥MB,
∵根据点M与点P的位置可知,点M与点P的水平距离为8﹣3=5,
∴点Q与点B的水平距离为5,即点Q的横坐标为﹣7,
在抛物线C1中,当x=﹣7时,y=﹣ ![]() ,即Q(﹣7,﹣
,即Q(﹣7,﹣ ![]() ),
),
∵根据点M与点B的位置可知,点M与点B的铅垂距离为 ![]() ,
,
∴点Q与点P的铅垂距离为 ![]() ,即点P离y轴的距离为
,即点P离y轴的距离为 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴P(3,﹣ ![]() );
);
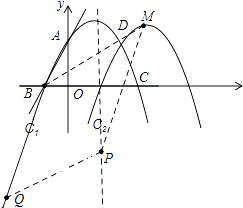
③如图,当四边形PQMB为平行四边形时,PQ∥BM,
∵根据点B与点P的位置可知,点B与点P的水平距离为3﹣(﹣2)=5,
∴点Q与点M的水平距离为5,即点Q的横坐标为8+5=13,
在抛物线C1中,当x=13时,y=﹣ ![]() ,即Q(13,﹣
,即Q(13,﹣ ![]() ),
),
∵根据点M与点Q的位置可知,点M与点Q的铅垂距离为 ![]() ﹣(﹣
﹣(﹣ ![]() )=25,
)=25,
∴点B与点P的铅垂距离为25,即点P离y轴的距离为25,
∴P(3,﹣25).
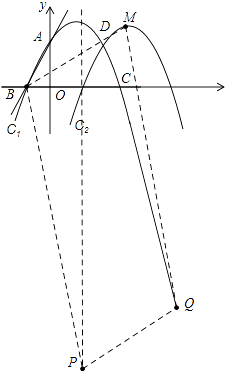
【解析】本题主要考查了二次函数的综合运用,综合性较强,需要综合运用待定系数法求函数解析式,平行四边形的判定和性质,直角三角形的判定和性质等知识.在解题时要利用数形结合的思想把代数和几何图形结合起来,要注意分类讨论思想的应用.(1)先根据直线y=2x+4,求得点A和点B的坐标,再根据抛物线C1过A、B两点,运用待定系数法即可求得抛物线解析式,最后令y=0,求得C点坐标;(2)先证明△ABC是直角三角形,求得△ABC的斜边BC的中点E的坐标,再结合F点坐标求得抛物线C2的解析式,再联立方程组并解出交点D的坐标,最后根据S四边形AOCD=S△AOD+S△OCD , 即可得出四边形AOCD的面积;(3)根据以点M、Q、P、B为顶点的四边形为平行四边形,分情况讨论可能的情形,根据平行四边形顶点的位置即可得出P点坐标.
【考点精析】本题主要考查了平行四边形的判定与性质和平移的性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60(
 +
+ 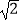 )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(
)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(  -
- 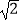 )海里.
)海里.
(参考数据: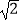 =1.41,
=1.41,  =1.73,
=1.73,  =2.45)
=2.45)
(1)分别求出A与C及B与C的距离AC、BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
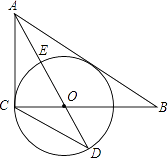
(1)求证:AB是⊙O的切线.
(2)已知AO角⊙O于点E,延长AO交⊙O于点D,tanD= ,求
,求 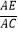 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式.
(2)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人.问:这天宾馆入住的游客人数最少有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式组
 ,其解集在数轴上表示正确的是( )
,其解集在数轴上表示正确的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(﹣3,6),B(﹣9,﹣3),以原点O为位似中心,相似比为
 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2)
B.(﹣9,18)
C.(﹣9,18)或(9,﹣18)
D.(﹣1,2)或(1,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
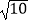 ,BC边上的高AD=6,则另一边BC等于( )
,BC边上的高AD=6,则另一边BC等于( )
A.10
B.8
C.6或10
D.8或10
相关试题

