【题目】已知直线![]() ,
,
(1)如图1,点![]() 在直线
在直线![]() 上的左侧,直接写出
上的左侧,直接写出![]() ,
,![]() 和
和![]() 之间的数量关系是 .
之间的数量关系是 .
(2)如图2,点![]() 在直线
在直线![]() 的左侧,
的左侧,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,直接写出
,直接写出![]() 和
和![]() 的数量关系是 .
的数量关系是 .
(3)如图3,点![]() 在直线
在直线![]() 的右侧
的右侧![]() ,
,![]() 仍平分
仍平分![]() ,
,![]() ,那么
,那么![]() 和
和![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.

参考答案:
【答案】(1) ![]() ;(2)
;(2)![]() ;
;
(3)![]() .理由见解析
.理由见解析
【解析】
(1)首先作EF∥AB,根据直线AB∥CD,可得EF∥CD,所以∠ABE=∠1,∠CDE=∠2,据此推得∠ABE+∠CDE=∠BED即可.
(2)首先根据BF,DF分别平分∠ABE,∠CDE,推得∠ABF+∠CFD=![]() (∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CFD,∠BED=∠ABE+∠CDE,据此推得∠BFD=
(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CFD,∠BED=∠ABE+∠CDE,据此推得∠BFD=![]() ∠BED.
∠BED.
(3)首先过点E作EG∥CD,再根据AB∥CD,EG∥CD,推得AB∥CD∥EG,所以∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,据此推得∠ABE+∠CDE+∠BED=360°;然后根据∠BFD=∠ABF+∠CDF,以及BF,DF分别平分∠ABE,∠CDE,推得2∠BFD+∠BED=360°即可.
解:(1)如图1,作![]() ,
,
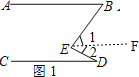 ,
,
![]() 直线
直线![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即![]() .
.
(2)如图2,
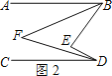 ,
,
![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
由(1),可得
![]()
![]() ,
,
![]() .
.
(3)如图3,过点![]() 作
作![]() ,
,
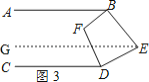 ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
由(1)知,![]() ,
,
又![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
故答案为:![]() 、
、![]() .
.
-
科目: 来源: 题型:
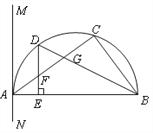
查看答案和解析>>【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。
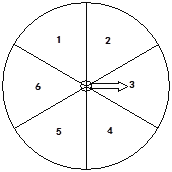
其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某汽车行驶的路程

 与时间
与时间 (分钟)的函数关系图.
(分钟)的函数关系图.
观察图中所提供的信息,解答下列问题:
(1)汽车在前
 分钟内的平均速度是 .
分钟内的平均速度是 .(2)汽车在中途停了多长时间?
(3)当
 时,求
时,求 与
与 的函数关系式
的函数关系式 -
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=kx+b的自变量x的取值范围是-2≤x≤6,相应的函数值的范围是-11≤y≤9,求此函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )

A.120°B.135°C.150°D.不能确定
相关试题

