【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )

A.120°B.135°C.150°D.不能确定
参考答案:
【答案】B
【解析】
先根据∠1+∠2=90°得出∠EAM+∠EDN的度数,再由角平分线的定义得出∠EAF+∠EDF的度数,根据AE⊥DE可得出∠3+∠4的度数,进而可得出∠FAD+∠FDA的度数,由三角形内角和定理即可得出结论.
解:

∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=![]() ×270°=135°.
×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 ,
,(1)如图1,点
 在直线
在直线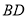 上的左侧,直接写出
上的左侧,直接写出 ,
, 和
和 之间的数量关系是 .
之间的数量关系是 .(2)如图2,点
 在直线
在直线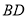 的左侧,
的左侧,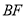 ,
, 分别平分
分别平分 ,
, ,直接写出
,直接写出 和
和 的数量关系是 .
的数量关系是 .(3)如图3,点
 在直线
在直线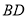 的右侧
的右侧 ,
, 仍平分
仍平分 ,
, ,那么
,那么 和
和 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某汽车行驶的路程

 与时间
与时间 (分钟)的函数关系图.
(分钟)的函数关系图.
观察图中所提供的信息,解答下列问题:
(1)汽车在前
 分钟内的平均速度是 .
分钟内的平均速度是 .(2)汽车在中途停了多长时间?
(3)当
 时,求
时,求 与
与 的函数关系式
的函数关系式 -
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=kx+b的自变量x的取值范围是-2≤x≤6,相应的函数值的范围是-11≤y≤9,求此函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的交点Q的纵坐标为4.
(1)求这两个函数的解析式;
(2)在同一直角坐标系中画出这两个函数的图象;
(3)求△PQO的面积.

-
科目: 来源: 题型:
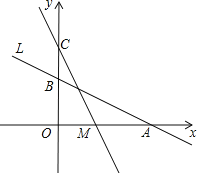
查看答案和解析>>【题目】如图,直线L:y=﹣
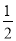 x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式6-2(x+1)≤3(x-2).
(2)解不等式组
 ,并写出该不等式组的整数解.
,并写出该不等式组的整数解.
相关试题

