【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.
(1)该顾客至少可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
参考答案:
【答案】
(1)10
(2)解:画树状图如下:
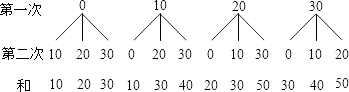
从上图可以看出,共有12种可能结果,其中大于或等于30元共有8种可能结果,
因此P(不低于30元)= ![]() .
.
【解析】(1)如果摸到0元和10元的时候,得到的购物券是最少,一共10元。
(2)根据第一次摸出后不放回,采用列表法或画树状图法可以不重复不遗漏地列出所有可能的结果,再求出不低于30元的可能数,利用概率公式即可求解。
【考点精析】本题主要考查了列表法与树状图法和概率公式的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个由正方形ABCD和半圆O组成的封闭图形,点O是圆心.点P从点A出发,沿线段AB,弧BC和线段CD匀速运动,到达终点D.运动过程中OP扫过的面积(s)随时间(t)变化的图象大致是( )
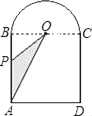
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩
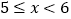
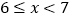
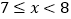
合计
频数
3
27
9
m
1
n
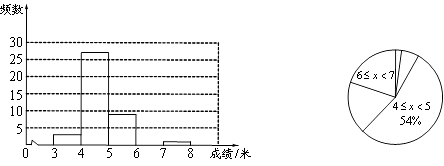
请你结合图表中所提供的信息,回答下列问题:
(1)表中m= , n=;
(2)请补全频数分布直方图;
(3)在扇形统计图中,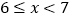 这一组所占圆心角的度数为度;
这一组所占圆心角的度数为度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据:
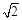 ≈1.41).
≈1.41).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一直线的两条直线互相平行;④平行于同一直线的两条直线互相平行;⑤两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线互相平行;⑥连结
 、
、 两点的线段就是
两点的线段就是 、
、 两点之间的距离,其中正确的有( )
两点之间的距离,其中正确的有( )A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 (元)与销售单价
(元)与销售单价  (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
相关试题

