【题目】某集团购买了150吨物资打算运往某地支援,现有甲、乙、丙三种车型供选择,每辆汽车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 1000 | 1200 | 1500 |
(1)若全部物资都用甲、乙两种车型来运送,需运费24000元,问分别需甲、乙两种车型各多少辆?
(2)若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送,请你写出可能的运送方案,并帮助该集团找出运费最省的方案(甲、乙、丙三种车辆均要参与运送).
参考答案:
【答案】(1)需甲种车型6辆,乙种车型15辆;(2)可能的运送方案有两种:方案一,需甲种车型4辆,乙种车型5辆,丙种车型9辆;方案二,需甲种车型2辆,乙种车型10辆,丙种车型6辆.方案二的运费最省,运费为23000元.
【解析】
(1)设需甲种车型x辆,乙种车型y辆,然后根据物资总重量和总运费建立方程组,求解即可得;
(2)设需甲种车型a辆,乙种车型b辆,则需丙种车型![]() 辆,再根据总重量得出关于a、b的等式,然后根据正整数性求出a、b的值,最后根据汽车费用表求解即可.
辆,再根据总重量得出关于a、b的等式,然后根据正整数性求出a、b的值,最后根据汽车费用表求解即可.
(1)设需甲种车型x辆,乙种车型y辆
由题意得:![]()
解得:![]()
答:需甲种车型6辆,乙种车型15辆;
(2)设需甲种车型a辆,乙种车型b辆,其中a、b为正整数,则需丙种车型![]() 辆
辆
由题意得:![]()
整理得:![]() ,即
,即![]()
![]() 均为正整数
均为正整数
![]() 或
或![]()
①当![]() 时,
时,![]() ,
,![]()
则总运费为![]() (元)
(元)
②当![]() 时,
时,![]() ,
,![]()
则总运费为![]() (元)
(元)
综上,可能的运送方案有两种:方案一,需甲种车型4辆,乙种车型5辆,丙种车型9辆;方案二,需甲种车型2辆,乙种车型10辆,丙种车型6辆.方案二的运费最省,运费为23000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,小明量出AB=26cm,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有A型、B型正方形卡片和C型长方形卡片各若干张.

(1)用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式____;
(2)选取1张A型卡片,10张C型卡片,____张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为____;
(3)如图3,两个正方形边长分别为m、n,m+n=10,mn=19,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.

(1)当t为何值时,FC与EG互相平分;
(2)连接FG,当t<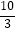 时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
(3)设△EFG的面积为y,求出y与t的函数关系式,求当t为何值时,y有最大值?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.

(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然事件是( )
A.抛掷1个均匀的骰子,出现6点向上
B.两直线被第三条直线所截,同位角相等
C.366人中至少有2人的生日相同
D.实数的绝对值是非负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
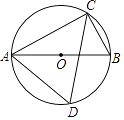
A.25
B.30°
C.45°
D.65°
相关试题

