【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=![]() ,BE=
,BE=![]() .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.

参考答案:
【答案】解:如图,过点D作DH⊥AC,

∵∠CED=45°,DH⊥EC,DE=![]() ,∴EH=DH。
,∴EH=DH。
∵EH2+DH2=ED2,∴EH2=1。∴EH=DH=1。
又∵∠DCE=30°,∴CD=2,HC=![]() 。
。
∵∠AEB=45°,∠BAC=90°,BE=![]() 。∴AB=AE=2。
。∴AB=AE=2。
∴AC=2+1+![]() =3+
=3+![]() 。
。
∴S四边形ABCD=![]() ×2×(3+
×2×(3+![]() )+
)+![]() ×1×(3+
×1×(3+![]() )=
)=![]() 。
。
【解析】利用等腰直角三角形的性质得出EH=DH=1,进而得出再利用直角三角形中30°所对边等于斜边的一半得
出CD的长,求出AC,AB的长即可得出四边形ABCD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】李大爷一年前买入了A、B两种兔子共46只.目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只.
(1)则一年前李大爷买入A种兔子________只,目前A、B两种兔子共________只(用含a的代数式表示);
(2)若一年前买入的A种兔子数量多于B种兔子数量,则目前A、B两种兔子共有多少只?
(3)李大爷目前准备卖出30只兔子,已知卖A种兔子可获利15元/只,卖B种兔子可获利6元/只.如果卖出的A种兔子少于15只,且总共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?请求出最大获利.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是关于x的二次函数,求:
是关于x的二次函数,求: (1)满足条件m的值。
(2)m为何值时,抛物线有最底点?求出这个最底点的坐标,这时
 为何值时y随
为何值时y随 的增大而增大?
的增大而增大?(3)m为何值时,抛物线有最大值?最大值是多少?这时
 为何值时,y随
为何值时,y随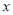 的增大而减小.
的增大而减小. -
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图,不写作法,但要求保留作图痕迹.

(1)已知:线段a和∠α,如图.求作:△ABC,使得AB=a,∠ABC=∠α.∠BAC=2∠α.
(2)在(1)的条件下,若∠ABC=360,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图AO和BD相交于点O,E是CD上一点,F是OD上一点,EF∥OC,∠1=∠A
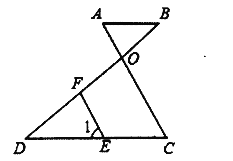
(1)试判断AB和CD的位置关系,并说明理由;
(2)若∠B=50°,∠1=65°,求∠DOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中装有2个红球,1个黄球,它们除颜色外其余都相同. 小明和小张做摸球游戏,约定一次游戏规则是:小张先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同,小张赢,否则小明赢.
(1)请用树状图或列表格法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则对双方公平吗?请说明理由.
相关试题

