【题目】已知,如图AO和BD相交于点O,E是CD上一点,F是OD上一点,EF∥OC,∠1=∠A
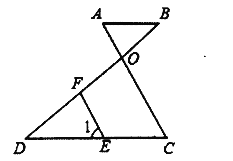
(1)试判断AB和CD的位置关系,并说明理由;
(2)若∠B=50°,∠1=65°,求∠DOC的度数.
参考答案:
【答案】(1)平行,理由见解析;(2)65o
【解析】
(1)由平行线的性质可得∠1=∠C,结合∠1=∠A,则有∠C=∠A,根据内错角相等,两直线平行得到AB//DC;
(2)由∠1=∠A可得:∠A=65°,在△AOB中∠B=50°,再根据三角形内角和定理求得∠AOB的度数,从而求得∠DOC的度数.
(1)AB//CD,
理由如下:
∵OC//EF,
∴∠1=∠C,
又∵∠1=∠A,
∴∠1=∠C,
∴AB//DC;
(2)∵∠1=65°,∠1=∠A,
∴∠A=65°,
又∵∠B=50°,
∴∠AOB=180o-(∠A+∠B)=65o.
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图,不写作法,但要求保留作图痕迹.

(1)已知:线段a和∠α,如图.求作:△ABC,使得AB=a,∠ABC=∠α.∠BAC=2∠α.
(2)在(1)的条件下,若∠ABC=360,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=
 ,BE=
,BE= .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)

-
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中装有2个红球,1个黄球,它们除颜色外其余都相同. 小明和小张做摸球游戏,约定一次游戏规则是:小张先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同,小张赢,否则小明赢.
(1)请用树状图或列表格法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则对双方公平吗?请说明理由.
-
科目: 来源: 题型:
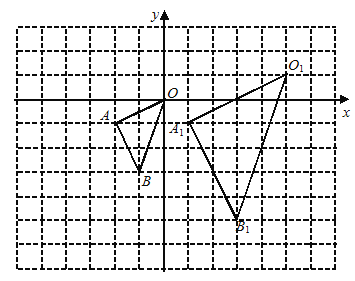
查看答案和解析>>【题目】在下图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1. 并写出点B的对应点B2的坐标;
(3)△OAB 内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标;
(4)判断△OA2B2能否看作是由△O1A1B1经过某种变换后得到的图形,若是,请指出是怎样变换得到的(直接写答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,∠B=90°,AB=16cm,AC=20cm,P、Q是△ABC的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.
(1)则BC= cm;
(2)当t为何值时,点P在边AC的垂直平分线上?此时CQ= ;
(3)当点Q在边CA上运动时,直接写出使△BCQ成为等腰三角形的运动时间.

相关试题

