【题目】李大爷一年前买入了A、B两种兔子共46只.目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只.
(1)则一年前李大爷买入A种兔子________只,目前A、B两种兔子共________只(用含a的代数式表示);
(2)若一年前买入的A种兔子数量多于B种兔子数量,则目前A、B两种兔子共有多少只?
(3)李大爷目前准备卖出30只兔子,已知卖A种兔子可获利15元/只,卖B种兔子可获利6元/只.如果卖出的A种兔子少于15只,且总共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?请求出最大获利.
参考答案:
【答案】(1)![]() ,43-a;(2) 当a=1时,A、B两种兔子有42只;(3) 方案一:卖出的A种兔子12只,B种兔子18只,可获利12×15+18×6=288(元),方案二:卖出的A种兔子13只,B种兔子17只,可获利13×15+17×6=297(元),方案三:卖出的A种兔子14只,B种兔子16只,可获利14×15+16×6=306(元),方案三获利最大,最大利润为306元
,43-a;(2) 当a=1时,A、B两种兔子有42只;(3) 方案一:卖出的A种兔子12只,B种兔子18只,可获利12×15+18×6=288(元),方案二:卖出的A种兔子13只,B种兔子17只,可获利13×15+17×6=297(元),方案三:卖出的A种兔子14只,B种兔子16只,可获利14×15+16×6=306(元),方案三获利最大,最大利润为306元
【解析】
(1)利用目前他所养的这两种兔子数量相同,得出等式求解即可;(2)利用一年前买入的兔子数量多于B种兔子数量,得出不等式求解即可;(3)利用总共获利不低于280元,卖A种兔子可获利15元/只,卖B种兔子可获利6元/只,得出不等关系,进而利用A种兔子的数量取值范围得出即可.
(1)![]() ;43﹣a
;43﹣a
(2)解:由题意得出:![]() >
>![]() , 解得:a<3,
, 解得:a<3,
由题意得:a,![]() ,
,![]() 应为正整数,
应为正整数,
当a=1时,符合题意,即目前A、B两种兔子有42只;
当a=2时,![]() ,
,![]() 为分数,不合题意;
为分数,不合题意;
∴当a=1时,A、B两种兔子有42只
(3)解:设李大爷卖出A种兔子y只,则卖出B种兔子(30﹣y)只,由题意得出: 15y+(30﹣y)×6≥280,
解得:y≥![]() ,
,
又∵卖出的A种兔子少于15只,即 ![]() ≤y<15,
≤y<15,
∵y是整数,
∴y=12,13,14,即李大爷有三种卖兔方案:
方案一:卖出的A种兔子12只,B种兔子18只,可获利12×15+18×6=288(元),
方案二:卖出的A种兔子13只,B种兔子17只,可获利13×15+17×6=297(元),
方案三:卖出的A种兔子14只,B种兔子16只,可获利14×15+16×6=306(元),
显然,方案三获利最大,最大利润为306元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.

(1)画出将△ABC向右平移2个单位后得到的△A1B1C1 , 再画出将△A1B1C1绕点B1按逆时针方向旋转90°后所得到的△A2B1C2;
(2)求线段B1C1旋转到B1C2的过程中,点C1所经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过点A(0,3)、B(4,3)、C(1,0)、
(1)填空:抛物线的对称轴为直线x= , 抛物线与x轴的另一个交点D的坐标为;
(2)求该抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】石头剪子布,又称“猜丁壳”,是一种起源于中国流传多年的猜拳游戏,游戏时的各方每次用一只手做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头”.两人游戏时,若出现相同手势,则不分胜负游戏继续,直到分出胜负,游戏结束,三人游戏时,若三种手势都相同或都不相同,则不分胜负游戏继续,若出现两人手势相同,则视为一种手势与第三人所出手势进行对决,此时,参照两人游戏规则,例如甲、乙二人同时出石头,丙出剪刀,则甲、乙获胜,假定甲、乙、丙三人每次都是随机地做这三种手势,那么:
(1)直接写出一次游戏中甲、乙两人出第一次手势时,不分胜负的概率;
(2)请你画出树状图求出一次游戏中甲、乙、丙三人出第一次手势时,不分胜负的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣
 ≤x<n+
≤x<n+  ,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题: (1)填空:
①若[x]=3,则x应满足的条件:________;
②若[3x+1]=3,则x应满足的条件:________;
(2)求满足[x]=
 x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为<x>,即:当n为非负整数时,如果n﹣
 ≤x<n+
≤x<n+  ,则<x>=n. 如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
,则<x>=n. 如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…试解决下列问题:
(1)填空:①<π>=________;②如果<2x﹣1>=3,则实数x的取值范围为________;
(2)①当x≥0,m为非负整数时,求证:<x+m>=m+<x>;②举例说明<x+y>=<x>+<y>不恒成立;
(3)求满足<x>=
 x的所有非负实数x的值.
x的所有非负实数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解一元二次不等式
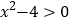 .
.请按照下面的步骤,完成本题的解答.
解:
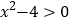 可化为
可化为  .
. (1)依据“两数相乘,同号得正”,可得不等式组①
 或不等式组②________.
或不等式组②________. (2)解不等式组①,得________.
(3)解不等式组②,得________.
(4)一元二次不等式
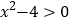 的解集为________.
的解集为________.
相关试题

