【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

参考答案:
【答案】(1)①全等,理由见解析;②![]() cm/s;(2)经过
cm/s;(2)经过![]() s点P与点Q第一次在边AB上相遇.
s点P与点Q第一次在边AB上相遇.
【解析】
(1)①根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等.
②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个腰长.
(1)①∵t=1s,∴BP=CQ=3×1=3cm.
∵AB=10cm,点D为AB的中点,∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,∴PC=8﹣3=5cm,∴PC=BD.
又∵AB=AC,∴∠B=∠C,
在△BPD和△CQP中,
 ,
,
∴△BPD≌△CQP(SAS).
②∵vP≠vQ,∴BP≠CQ,
若△BPD≌△CPQ,∠B=∠C,
则BP=PC=4cm,CQ=BD=5cm,∴点P,点Q运动的时间![]() s,
s,
∴ cm/s;
cm/s;
(2)设经过x秒后点P与点Q第一次相遇,
由题意,得![]() x=3x+2×10,
x=3x+2×10,
解得:![]() ,
,
∴点P共运动了![]() ×3=80cm.
×3=80cm.
△ABC周长为:10+10+8=28cm,
若是运动了三圈即为:28×3=84cm.
∵84﹣80=4cm<AB的长度,
∴点P、点Q在AB边上相遇,
∴经过![]() s点P与点Q第一次在边AB上相遇.
s点P与点Q第一次在边AB上相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.

解:∵∠1=∠B
∴AD∥( )(内错角相等,两直线平行)
∴∠C+∠2=180°,( )
∵∠C=110°.
∴∠2=( )°.
∴∠3=∠2=70°.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量t(件),与每件的销售价x(元/件)可看成是一次函数关系:t=-3x+204.
(1)写出商场卖这种服装每天的销售利润
 与每件的销售价
与每件的销售价 之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
-
科目: 来源: 题型:
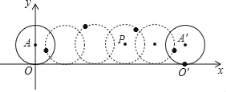
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径为1的圆从原点出发沿x轴正方向滚动一周,圆上一点由原点O到达点O′,圆心也从点A到达点A′.
(1)点O′的坐标为 ,点A′的坐标为 ;
(2)若点P是圆在滚动过程中圆心经过的某一位置,求以点P,点O,点O′为顶点的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的顶点B、C在x轴的正半轴上,反个比例函数y=
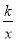 (k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n, 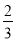 ),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
),过点E作直线l∥BD交y轴于点F,则点F的坐标是( ) 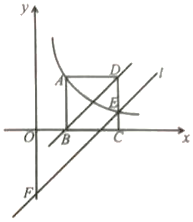
A. (0,-
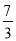 )B. (0,-
)B. (0,- 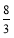 )
)C. (0,-3)D. (0,-
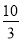 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2015年底拥有家庭轿车64辆,2017年底家庭轿车的拥有量达到100辆.
(1)若该小区2015年底到2018年底家庭轿车拥有量的年平均增长率都相同,求该小区到2018年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
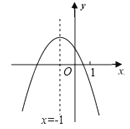
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

