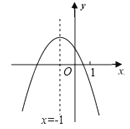
【题目】.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】解:∵抛物线和x轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2<0,∴①正确;
∵对称轴是直线x=﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,∴4a+c>2b,∴②错误;
∵把x=1代入抛物线得:y=a+b+c<0,∴2a+2b+2c<0,∵ ![]() =﹣1,∴b=2a,∴3b+2c<0,∴③正确;
=﹣1,∴b=2a,∴3b+2c<0,∴③正确;
∵抛物线的对称轴是直线x=﹣1,∴y=a﹣b+c的值最大,即把x=m(m≠﹣1)代入得:y=am2+bm+c<a﹣b+c,∴am2+bm+b<a,即m(am+b)+b<a,∴④正确;
即正确的有3个,故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的顶点B、C在x轴的正半轴上,反个比例函数y=
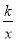 (k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n, 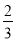 ),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
),过点E作直线l∥BD交y轴于点F,则点F的坐标是( ) 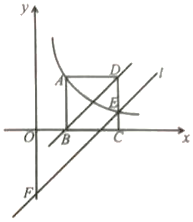
A. (0,-
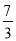 )B. (0,-
)B. (0,- 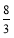 )
)C. (0,-3)D. (0,-
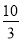 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2015年底拥有家庭轿车64辆,2017年底家庭轿车的拥有量达到100辆.
(1)若该小区2015年底到2018年底家庭轿车拥有量的年平均增长率都相同,求该小区到2018年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正比例函数的图像与反比例函数
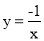 交于A(x1,y1),B(x2,y2),那么(x1-x2)(y1-y2)=____________.
交于A(x1,y1),B(x2,y2),那么(x1-x2)(y1-y2)=____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,
, 是对角线
是对角线 上的一个动点,若
上的一个动点,若 的最小值是10,则
的最小值是10,则 长为___________.
长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如下(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中D小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?

相关试题

