【题目】阅读下面材料:
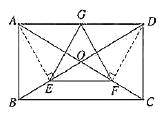
小明遇到这样一个问题: 如图1,在矩形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接所
的中点,连接所![]() 、
、![]() 、
、![]() .
.
求证:![]() 是等边三角形.
是等边三角形.
小明经探究发现,连接![]() 、
、![]() (如图2),从而可证
(如图2),从而可证![]() ,
, ![]() ,使问题得到解决.
,使问题得到解决.

(1)请你按照小明的探究思路,完成他的证明过程;
参考小明思考问题的方法或用其他的方法,解决下面的问题:
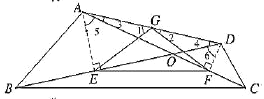
(2)如图3,在四边形![]() 中,
中, ![]() ,
,![]() , 对角线
, 对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() (
(![]() ),点
),点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() .
.
①否存在与![]() 相等的线段?若存在,请找出并证明;若不存在,说明理由.
相等的线段?若存在,请找出并证明;若不存在,说明理由.
②求![]() 的度数.(用含
的度数.(用含![]() 的式子表示)
的式子表示)
参考答案:
【答案】(1)见解析;(2)①![]() ,证明见解析;②
,证明见解析;②![]()
![]() .
.
【解析】
(1)如图,连接![]() 、
、![]() ,由已知条件可证明
,由已知条件可证明![]() 是等边三角形,进而证明
是等边三角形,进而证明![]() 是直角三角形,根据
是直角三角形,根据![]() 为AD的中点,证明
为AD的中点,证明![]() ,再由三角形中位线定理,即可证明结论;
,再由三角形中位线定理,即可证明结论;
(2)①如图,![]() ,类比(1)即可证明结论;
,类比(1)即可证明结论;
②如图,![]()
![]() .根据①结论得到
.根据①结论得到![]() ,再得到
,再得到![]() ,进而证明
,进而证明![]() ,
,![]() ,最后求出
,最后求出![]() ,问题得解.
,问题得解.
(1)证明:如图,连接![]() 、
、![]() ,
,
∵四边形![]() 为炬形,
为炬形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
∴![]() 是直角三角形.
是直角三角形.
∵![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
∵点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() .
.
∴![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
(2)①![]() .
.
证明:如图,连接![]() 、
、![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() 是等腰三角形
是等腰三角形
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
∴![]() 是直角三角形、
是直角三角形、
∵![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
同理可得![]() .
.
∴![]() .
.
②解:∵![]() ,
,![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴同理可得![]() .
.
∴![]() .
.
由①可知,![]() ,
,![]() ,
,
∴![]() ,
,
![]() .
.
∴![]() .
.
![]()
![]() .
.
∴![]()
![]()
![]() .
.
∴![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=cm.

-
科目: 来源: 题型:
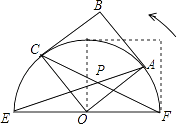
查看答案和解析>>【题目】如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10t;用1辆A型车和2辆B型车装满货物一次可运货11t.某物流公司现有35t货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市在招商引资期间,把已经破产的油泵厂出租给外地某投资商,该投资商为了减少固定资产投资,将原来400平方米的正方形场地建成300平方米的长方形场地,并且长、宽的比为5:3,并且把原来的正方形铁栅栏围墙全部利用,围成新场地的长方形围墙,请问这些铁栅栏是否够用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC=8,∠BAC=30°,将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
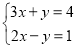 ;
;(2)
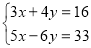 ;
;(3)
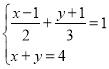 .
.
相关试题

