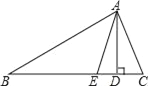
【题目】已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠ABC=30°,∠ACB=50°.
(1)求∠DAE的度数;
(2)写出∠DAE与∠ACB﹣∠ABC的数量关系: ,并证明你的结论.
参考答案:
【答案】(1)∠DAE=10°;(2)∠DAE=![]() (∠ACB﹣∠ABC),理由见解析.
(∠ACB﹣∠ABC),理由见解析.
【解析】试题分析:(1)先根据三角形内角和得到∠CAB=180°﹣∠B﹣∠C=100°,再根据角平分线与高线的定义得到∠CAE=![]() ∠CAB=50°,∠ADC=90°,则∠CAD=90°﹣∠C=40°,然后利用∠DAE=∠CAE﹣∠CAD计算即可.
∠CAB=50°,∠ADC=90°,则∠CAD=90°﹣∠C=40°,然后利用∠DAE=∠CAE﹣∠CAD计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C﹣∠B的关系.
试题解析:(1)∵∠ABC=30°,∠ACB=50°,
∴∠CAB=180°﹣∠B﹣∠C=100°,
∵AE是△ABC角平分线,
∴∠CAE=![]() ∠CAB=50°,
∠CAB=50°,
∵AD分别是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=40°,
∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°.
(2)∠DAE=![]() (∠ACB﹣∠ABC),
(∠ACB﹣∠ABC),
理由:∵在△ABC中,AD,AE分别是△ABC的高和角平分线,
∴∠CAB=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,∠CAE=![]() (180°﹣∠B﹣∠C),
(180°﹣∠B﹣∠C),
∴∠DAE=![]() (180°﹣∠B﹣∠C)﹣(90°﹣∠C)=
(180°﹣∠B﹣∠C)﹣(90°﹣∠C)=![]() (∠C﹣∠B).
(∠C﹣∠B).
-
科目: 来源: 题型:
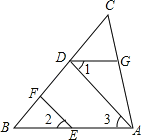
查看答案和解析>>【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= (等量代换)
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵∠CAB=70° ,(已知)
∴∠AGD= (等式性质)
-
科目: 来源: 题型:
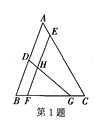
查看答案和解析>>【题目】如图,D、E、F、G四点在△ABC的三边上,其中DG与EF相交于点H.若 ∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列三角形相似的是( )
A.△BDG,△CEF B.△ABC,△CEF C.△ABC,△BDG D.△FGH,△ABC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在边AC上,下列条件中,能判断△BDC与△ABC相似的是 ( )

A. AB·CB=CA·CD B. AB·CD=BD·BC C. BC2=AC·DC D. BD2=CD·DA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)请计算△ABC的面积;
(3)直接写出△ABC关于x轴对称的三角形△A2B2C2的各点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,E的线段AD(除去端点A、D)上一动点,EF⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,求∠C的度数.
(2)当E在AD上移动时,∠B、∠C、∠DEF之间存在怎样的等量关系?请写出这个等量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】南充某制衣厂现有22名制作服装的工人,每天都制作某种品牌的衬衫和裤子,每人每天可制作这种衬衫3件或裤子5条。
(1)若该厂要求每天制作的衬衫和裤子配套,一件衬衫配两条裤子,则应各安排多少人分别制作衬衫和裤子?
(2)已知制作一件衬衫可获得利润30元,制作一条裤子可获得利润16元,在(1)的条件下,求该厂每天制作衬衫和裤子所获得的利润?
相关试题

