【题目】如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,E的线段AD(除去端点A、D)上一动点,EF⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,求∠C的度数.
(2)当E在AD上移动时,∠B、∠C、∠DEF之间存在怎样的等量关系?请写出这个等量关系,并说明理由.

参考答案:
【答案】(1)∠C=60°.
(2)∠C-∠B=2∠DEF.理由见解析
【解析】试题分析:(1)已知:EF⊥BC,∠DEF=10°可以求得∠EDF的度数,∠EDF又是ABD的外角,已知∠B的度数,可求得∠BAD的值,AD平分∠BAC,所以∠BAC的值也可求出,从而求出∠C。(2)EF⊥BC,可得到∠EDF=90°-∠DEF,∠EDF又是ABD的外角,可得到∠BAD=∠EDF-∠B=90°-∠DEF-∠B,然后可将![]() BAC用含∠DEF、∠B的角来表示,即
BAC用含∠DEF、∠B的角来表示,即![]() BAC =2(90°-∠DEF-∠B),最后利用∠B、
BAC =2(90°-∠DEF-∠B),最后利用∠B、![]() BAC、
BAC、![]() C的和为180°求得三角之间的等量关系。
C的和为180°求得三角之间的等量关系。
试题解析:(1)∵EF⊥BC,∠DEF=10°,
∴∠EDF=80°.
∵∠B=40°,
∴∠BAD=∠EDF-∠B=80°-40°=40°.
∵AD平分∠BAC,∴∠BAC=80°.
∴∠C=180°-40°-80°=60°.
(2)∠C-∠B=2∠DEF.理由如下:
∵EF⊥BC,∴∠EDF=90°-∠DEF.
∵∠EDF=∠B+∠BAD,
∴∠BAD=90°-∠DEF-∠B.
∵AD平分∠BAC,
∴∠BAC=2∠BAD=180°-2∠DEF-2∠B.
∴∠B+180°-2∠DEF-2∠B+∠C=180°.
∴∠C-∠B=2∠DEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明打算用一块面积为900cm2的正方形木板,沿着边的方向裁出一个长方形面积为588cm2桌面,并且的长宽之比为4:3,你认为能做到吗?如果能,计算出桌面的长和宽;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上到﹣1点的距离等于1个单位的点所表示的数是( )
A. 0 B. ﹣1 C. 1或﹣1 D. 0或﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣3,﹣2),B(2,﹣2),C(3,1),D(﹣2,1)四个点.
(1)在图中描出A,B,C,D四个点,并顺次连接点A,B,C,D,A.
(2)直接写出线段AB,CD之间的关系.
(3)求四边形ABCD的面积.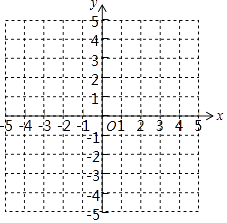
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,∠DAC=120°.

(1)若AB平分∠DAC,求∠ABC的度数.
(2)若∠ACF=20°,求∠BCF的度数.
(3)在(2)的条件下,若CE平分∠BCF,求∠CEF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等边三角形B.平行四边形C.正五边形D.圆
相关试题

