【题目】为贯彻党的“绿水青山就是金山银山”的理念,我市计划购买甲、乙两种树苗共7000株用于城市绿化,甲种树苗每株24元,一种树苗每株30元![]() 相关资料表明:甲、乙两种树苗的成活率分别为
相关资料表明:甲、乙两种树苗的成活率分别为![]() 、
、![]() .
.
![]() 若购买这两种树苗共用去180000元,则甲、乙两种树苗各购买多少株?
若购买这两种树苗共用去180000元,则甲、乙两种树苗各购买多少株?
![]() 若要使这批树苗的总成活率不低于
若要使这批树苗的总成活率不低于![]() ,则甲种树苗至多购买多少株?
,则甲种树苗至多购买多少株?
![]() 在
在![]() 的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
参考答案:
【答案】![]() 甲、乙两种树苗各购买5000、2000株;
甲、乙两种树苗各购买5000、2000株;![]() 甲种树苗至多购买2800株;
甲种树苗至多购买2800株;![]() 最少费用为
最少费用为![]() 元.
元.
【解析】
![]() 列方程求解即可;
列方程求解即可;
![]() 根据题意,甲乙两种树苗的存货量大于等于树苗总量的
根据题意,甲乙两种树苗的存货量大于等于树苗总量的![]() 列出不等式;
列出不等式;
![]() 用x表示购买树苗的总费用,根据一次函数增减性讨论最小值.
用x表示购买树苗的总费用,根据一次函数增减性讨论最小值.
![]() 设购买甲种树苗x株,则购买乙种树苗
设购买甲种树苗x株,则购买乙种树苗![]() 株,
株,
由题意得:![]()
解得![]() ,则
,则![]()
答:甲、乙两种树苗各购买5000、2000株;
![]() 根据题意得:
根据题意得:![]()
解得![]()
则甲种树苗至多购买2800株
![]() 设购买树苗的费用为W,
设购买树苗的费用为W,
根据题意得:![]()
![]()
![]() 随x的增大而减小
随x的增大而减小
![]() 当
当![]() 时,
时,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点
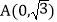 ,
,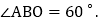 若对于平面内一点C,当
若对于平面内一点C,当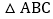 是以AB为腰的等腰三角形时,称点C时线段AB的“等长点”.
是以AB为腰的等腰三角形时,称点C时线段AB的“等长点”.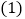 请判断点
请判断点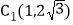 ,点
,点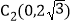 是否是线段AB的“等长点”,并说明理由;
是否是线段AB的“等长点”,并说明理由; 若点
若点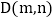 是线段AB的“等长点”,且
是线段AB的“等长点”,且 ,求m和n的值.
,求m和n的值.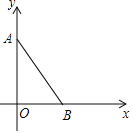
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
①最大的负整数是﹣1;②数轴上表示数2 和﹣2的点到原点的距离相等;③当a≤0时,|a|=﹣a成立;④a的倒数是
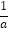 ;⑤(﹣2)2 和﹣22相等.
;⑤(﹣2)2 和﹣22相等.A. 2 个 B. 3 个 C. 4 个 D. 5 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
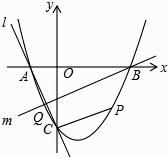
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,
 ,
,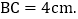 点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是
点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是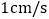 ,连接PQ、AQ、
,连接PQ、AQ、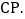 设点P、Q运动的时间为ts.
设点P、Q运动的时间为ts.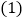 当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形ABQP是矩形;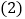 当t为何值时,四边形AQCP是菱形.
当t为何值时,四边形AQCP是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长都为 a 的正方形内分别排列着一些大小相等的圆:
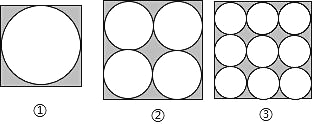
(1)根据图中的规律,第 4 个正方形内圆的个数是 ,第n 个正方形内圆的个数是_____.
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a 的代数式分别表示第 1 个正方形中、第 3 个正方形中阴影部分的面积(结果保留π);
②若 a=10,请直接写出第 2018 个正方形中阴影都分的面积 (结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=
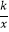 (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( ) 
A.y=
B.y=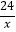
C.y=
D.y=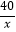
相关试题

