搜索
【题目】计算：
（1）
；
（2）
；
（3）
；
（4）
；
（5）（
）2；
（6）
；
（7）（
）（
）；
（8）
；
（9）
；
（10）
．
参考答案：
【答案】(1)4；（2）36
；（3）1；（4）3；（5）8+4
；（6）1；（7）-1；（8）
；（9）4+
；（10）6
.
【解析】
(1)直接利用
（a≥0，b≥0）计算可得答案；
（2）直接利用（a≥0，b≥0）计算可得答案；
（3）直接利用（a≥0，b≥0）计算再相减可得答案；
（4）先化简二次根式后计算除法可得答案；
（5）利用完全平方公式将原式展开后可得答案；
（6） 先化简二次根式后合并同类项后相除可得答案；
（7） 利用平方差公式将原式展开后可得答案；
（8）先化简二次根式后合并同类项后可得答案；
（9）先计算开平方开立方运算后相加减可得答案；
解：（1）
＝4；
（2）
；
（3）
＝6﹣5
＝1；
（4）
＝
＝3；
（5）
；
＝2+2××+6
＝8+4；
（6）
＝
＝1；
（7）
＝5﹣6
＝﹣1；
（8）
＝2-
-
＝
-
；
（9）
＝4﹣+2
＝4+；
（10）
＝9﹣3+
＝6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?
-
科目： 来源： 题型：
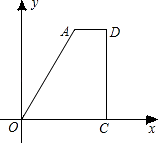
查看答案和解析>>【题目】如图，直角梯形AOCD的边OC在x轴上，O为坐标原点，CD垂直于x轴，D（5，4），AD=2．若动点E、F同时从点O出发，E点沿折线OA→AD→DC运动，到达C点时停止；F点沿OC运动，到达C点时停止，它们运动的速度都是每秒1个单位长度．设E运动x秒时，△EOF的面积为y（平方单位），则y关于x的函数图象大致为（ ）
A.
B.
C.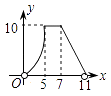
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，E在DC上，若DE：EC=1：2，则BF：EF= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，三角形ABC为一个电子跳蚤游戏盘，其中AB＝8，AC＝9，BC＝10.如果电子跳蚤开始时在BC边上的点P0处，BP0＝4，第一步跳蚤从点P0处跳到AC边上的点P1处，且CP1＝CP0；第二步跳蚤从点P1处跳到AB边上的点P2处，且AP1＝AP2；第三步跳蚤从点P2处跳回到BC边上的点P3处，且BP3＝BP2……若跳蚤按上述规则跳下去，第n次的落点为Pn，则点P3与点P2019之间的距离为( )
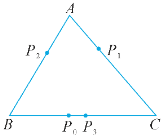
A. 0 B. 1 C. 4 D. 5
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC=10m，拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m2）．
（1）如图1，若BC=4m，则S=m2 ．
（2）如图2，现考虑在（1）中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，则在BC的变化过程中，当S取得最小值时，边BC的长为m． -
科目： 来源： 题型：
查看答案和解析>>【题目】[问题情境]勾股定理是一条古老的数学定理，它有很多种证明方法，我国汉代数学家赵爽根据弦图，利用面积法进行证明．著名数学家华罗庚曾提出把“数形关系(勾股定理)”带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．
[定理表述]请你根据图(1)中的直角三角形叙述勾股定理(用文字及符号语言叙述)．
[尝试证明]以图(1)中的直角三角形为基础，可以构造出以a、b为底，以a＋b为高的直角梯形(如图(2))，请你利用图(2)验证勾股定理．
[知识拓展]利用图(2)中的直角梯形，我们可以证明
．其证明步骤如下：∵BC＝a＋b，AD＝________，
又∵在直角梯形ABCD中，有BC________AD(填大小关系)，即________，
∴
．
相关试题
