【题目】[问题情境]勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明.著名数学家华罗庚曾提出把“数形关系(勾股定理)”带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]请你根据图(1)中的直角三角形叙述勾股定理(用文字及符号语言叙述).
[尝试证明]以图(1)中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图(2)),请你利用图(2)验证勾股定理.
[知识拓展]利用图(2)中的直角梯形,我们可以证明![]() .其证明步骤如下:
.其证明步骤如下:
∵BC=a+b,AD=________,
又∵在直角梯形ABCD中,有BC________AD(填大小关系),即________,
∴![]() .
.

参考答案:
【答案】见解析
【解析】
[定理表述]如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2.
[尝试证明]∵Rt△ABE≌Rt△ECD,∴∠AEB=∠EDC.
又∵∠EDC+∠DEC=90°,∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED,
∴![]() ,
,
整理,得a2+b2=c2.
[知识拓展]![]() ;<;
;<;![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 ;
;(2)
 ;
;(3)
 ;
;(4)
 ;
;(5)(
 )2;
)2;(6)
 ;
;(7)(
 )(
)( );
);(8)
 ;
;(9)
 ;
;(10)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC为一个电子跳蚤游戏盘,其中AB=8,AC=9,BC=10.如果电子跳蚤开始时在BC边上的点P0处,BP0=4,第一步跳蚤从点P0处跳到AC边上的点P1处,且CP1=CP0;第二步跳蚤从点P1处跳到AB边上的点P2处,且AP1=AP2;第三步跳蚤从点P2处跳回到BC边上的点P3处,且BP3=BP2……若跳蚤按上述规则跳下去,第n次的落点为Pn,则点P3与点P2019之间的距离为( )
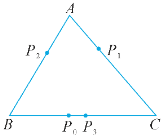
A. 0 B. 1 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m,拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).

(1)如图1,若BC=4m,则S=m2 .
(2)如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为m. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格MNPQ中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上.

(1)设正方形MNPQ网格内的每个小方格的边长为1,求:
①△ABQ,△BCM,△CDN,△ADP的面积;
②正方形ABCD的面积.
(2)设MB=a,BQ=b,利用这个图形中的直角三角形和正方形的面积关系,你能验证已学过的哪一个数学公式或定理吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:|﹣2|﹣(
 ﹣π)0+tan45°+(
﹣π)0+tan45°+(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在直角坐标系内的位置如图所示
(1)分别写出点A,C的坐标:A: ,C: ;
(2)△ABC的周长为 ,面积为 ;
(3)请在这个坐标系内画出△A1B1C1与△ABC关于x轴对称.

相关试题

