【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

参考答案:
【答案】由题意得AC="30m " AB=50m
∵∠ACB=90°
∴BC=![]()
∴小车行驶速度为40÷2=20米/秒
即为20×3600=72千米/小时
∵72千米/小时>70千米/小时
∴这辆小车超速了。
【解析】
(1)由题意知,△ABC为直角三角形,且AB是斜边,已知AB,AC根据勾股定理可以求BC;
(2)根据BC的长度和时间可以求小汽车在BC路程中的速度,若速度大于70千米/时,则小汽车超速;若速度小于70千米/时,则小汽车没有超速.
解:(1)由题意知,AB=130米,AC=50米,
且在Rt△ABC中,AB是斜边,
根据勾股定理AB2=BC2+AC2,
可以求得:BC=120米=0.12千米,
(2)∵6秒=![]() 小时,
小时,
∴速度为![]() =72千米/小时,
=72千米/小时,
故该小汽车超速.
答:该小汽车超速了,平均速度大于70千米/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=ax2+bx+4 与x轴交于点A(﹣3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线
y=ax2+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.数据4、5、5、6、0的平均数是5
B.数据2、3、4、2、3的众数是2
C.了解某班同学的身高情况适合全面调查
D.甲、乙两组数据的平均数相同,方差分别是S甲2=3.2,S乙2=2.9,则甲组数据更稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

-
科目: 来源: 题型:
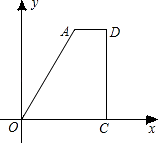
查看答案和解析>>【题目】如图,直角梯形AOCD的边OC在x轴上,O为坐标原点,CD垂直于x轴,D(5,4),AD=2.若动点E、F同时从点O出发,E点沿折线OA→AD→DC运动,到达C点时停止;F点沿OC运动,到达C点时停止,它们运动的速度都是每秒1个单位长度.设E运动x秒时,△EOF的面积为y(平方单位),则y关于x的函数图象大致为( )
A.
B.
C.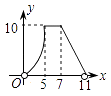
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E在DC上,若DE:EC=1:2,则BF:EF= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 ;
;(2)
 ;
;(3)
 ;
;(4)
 ;
;(5)(
 )2;
)2;(6)
 ;
;(7)(
 )(
)( );
);(8)
 ;
;(9)
 ;
;(10)
 .
.
相关试题

