【题目】安徽某水产养殖户去年利用“稻虾混养”使每千克小龙虾养殖成本降为6元,在整个销售旺季的80天里,销售单价P(元/千克)与时间第t(天)之间的函数关系为:P= ,日销售量y(千克)与时间第t(天)之间的函数关系如图所示.
,日销售量y(千克)与时间第t(天)之间的函数关系如图所示.
(1)求日销售y与时间t的函数关系式?
(2)设日销售利润为W(元),求W与t之间的函数表达式;
(3)日销售利润W哪一天最大?最大利润是多少?

参考答案:
【答案】(1) y=﹣2t+200(1≤t≤80,t为整数);(2) ①当1≤t≤40时,w=﹣![]() (t﹣30)2+2450.②当41≤t≤80时,w=﹣52t+5200;(3) 第41天的日销售利润最大,最大利润为3068元.
(t﹣30)2+2450.②当41≤t≤80时,w=﹣52t+5200;(3) 第41天的日销售利润最大,最大利润为3068元.
【解析】
①根据函数图象,利用待定系数法求解可得;
②设日销售利润为w,根据“总利润=每千克利润×销售量”列出函数解析式;
③根据第二问将二次函数配平方,从而求最值.
解:(1)设解析式为y=kt+b,
将(1,198)、(80,40)代入,得:![]() ,
,
解得:![]() ,
,
∴y=﹣2t+200(1≤t≤80,t为整数);
(2)设日销售利润为w,则w=(p﹣6)y,
①当1≤t≤40时,w=(![]() t+16﹣6)(﹣2t+200)=﹣
t+16﹣6)(﹣2t+200)=﹣![]() (t﹣30)2+2450.
(t﹣30)2+2450.
②当41≤t≤80时,w=26(﹣2t+200)=﹣52t+5200
(3)①当1≤t≤40时,w=﹣![]() (t﹣30)2+2450.
(t﹣30)2+2450.
∴当t=30时,w最大=2450;
②当41≤t≤80时,w=﹣52t+5200
∴当t=41时,w最大=3068,
∵3068>2450,
∴第41天的日销售利润最大,最大利润为3068元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=﹣x2﹣6x+21.求:
(1)直接写出抛物线y=﹣x2﹣6x+21的顶点坐标;
(2)当x>2时,求y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx(a≠0) 交x轴正半轴于点A,直线y=2x 经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.

(1)求a,b的值;
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m ,△OBP的面积为S,
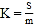 .求K关于m 的函数表达式及K的范围.
.求K关于m 的函数表达式及K的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3200米.甲同学先步行200米,然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的
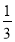 ,公交车的速度是乙骑自行车速度的3倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到8分钟.
,公交车的速度是乙骑自行车速度的3倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到8分钟.(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月
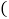 按30天计算
按30天计算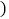 ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天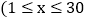 且x为整数
且x为整数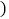 的销售量为y件.
的销售量为y件. 直接写出y与x的函数关系式;
直接写出y与x的函数关系式; 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=mx2+(2﹣2m)x+m﹣2(m是常数).
(1)无论m取何值,该抛物线都经过定点 D.直接写出点D的坐标.
(2)当m取不同的值时,该抛物线的顶点均在某个函数的图象上,求出这个函数的表达式.
(3)若在0≤x≤1的范围内,至少存在一个x的值,使y>0,求m的取值范围.
-
科目: 来源: 题型:
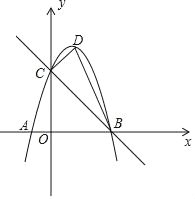
查看答案和解析>>【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
相关试题

