【题目】如图,C为射线AB上一点,AB=30,AC比BC的 ![]() 多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: ①BC=2AC;②AB=4NQ;③当PB=
多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: ①BC=2AC;②AB=4NQ;③当PB= ![]() BQ时,t=12,其中正确结论的个数是( )
BQ时,t=12,其中正确结论的个数是( )![]()
A.0
B.1
C.2
D.3
参考答案:
【答案】C
【解析】解:设BC=x, ∴AC= ![]() x+5
x+5
∵AC+BC=AB
∴x+ ![]() x+5=30,
x+5=30,
解得:x=20,
∴BC=20,AC=10,
∴BC=2AC,故①成立,
∵AP=2t,BQ=t,
当0≤t≤15时,
此时点P在线段AB上,
∴BP=AB﹣AP=30﹣2t,
∵M是BP的中点
∴MB= ![]() BP=15﹣t
BP=15﹣t
∵QM=MB+BQ,
∴QM=15,
∵N为QM的中点,
∴NQ= ![]() QM=
QM= ![]() ,
,
∴AB=4NQ,
当15<t≤30时,
此时点P在线段AB外,且点P在Q的左侧,
∴AP=2t,BQ=t,
∴BP=AP﹣AB=2t﹣30,
∵M是BP的中点
∴BM= ![]() BP=t﹣15
BP=t﹣15
∵QM=BQ﹣BM=15,
∵N为QM的中点,
∴NQ= ![]() QM=
QM= ![]() ,
,
∴AB=4NQ,
当t>30时,
此时点P在Q的右侧,
∴AP=2t,BQ=t,
∴BP=AP﹣AB=2t﹣30,
∵M是BP的中点
∴BM= ![]() BP=t﹣15
BP=t﹣15
∵QM=BQ﹣BM=15,
∵N为QM的中点,
∴NQ= ![]() QM=
QM= ![]() ,
,
∴AB=4NQ,
综上所述,AB=4NQ,故②正确,
当0<t≤15,PB= ![]() BQ时,此时点P在线段AB上,
BQ时,此时点P在线段AB上,
∴AP=2t,BQ=t
∴PB=AB﹣AP=30﹣2t,
∴30﹣2t= ![]() t,
t,
∴t=12,
当15<t≤30,PB= ![]() BQ时,此时点P在线段AB外,且点P在Q的左侧,
BQ时,此时点P在线段AB外,且点P在Q的左侧,![]()
∴AP=2t,BQ=t,
∴PB=AP﹣AB=2t﹣30,
∴2t﹣30= ![]() t,
t,
t=20,
当t>30时,此时点P在Q的右侧,![]()
∴AP=2t,BQ=t,
∴PB=AP﹣AB=2t﹣30,
∴2t﹣30= ![]() t,
t,
t=20,不符合t>30,
综上所述,当PB= ![]() BQ时,t=12或20,故③错误;
BQ时,t=12或20,故③错误;
故选(C)
根据AC比BC的 ![]() 多5可分别求出AC与BC的长度,然后分别求出当P与Q重合时,此时t=30s,当P到达B时,此时t=15s,最后分情况讨论点P与Q的位置.
多5可分别求出AC与BC的长度,然后分别求出当P与Q重合时,此时t=30s,当P到达B时,此时t=15s,最后分情况讨论点P与Q的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于四舍五入得到的近似数1.50万,下列说法中正确的是( )
A. 该近似数精确到百分位 B. 该近似数精确到十分位
C. 该近似数精确到千位 D. 该近似数精确到百位
-
科目: 来源: 题型:
查看答案和解析>>【题目】(13分)如图所示,四边形
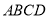 中,
中, 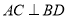 于点
于点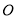 ,
, 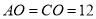 ,
, 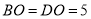 ,点
,点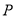 为线段
为线段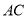 上的一个动点。
上的一个动点。(1)求证:
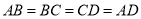 。
。(2)过点
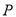 分别作
分别作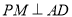 于
于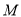 点,作
点,作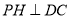 于
于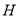 点。
点。① 试说明
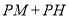 为定值。
为定值。② 连结
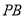 ,试探索:在点
,试探索:在点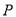 运动过程中,是否存在点
运动过程中,是否存在点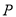 ,使
,使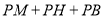 的值最小。若存在,请求出该最小值;若不存在,请说明理由。
的值最小。若存在,请求出该最小值;若不存在,请说明理由。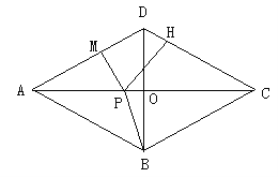
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上.
(1)如图1所示,若C的坐标是(2,0),点A的坐标是(﹣2,﹣2),求:点B的坐标;
(思路提示:过点A作AD⊥x轴于点D,通过证明△BOC≌△CDA来达到目的.)
(2)如图2,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴 于E,问BD与AE有怎样的数量关系,并说明理由;
(3)如图3,直角边BC的两个端点在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论①
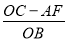 为定值;②
为定值;②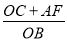 为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.
为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.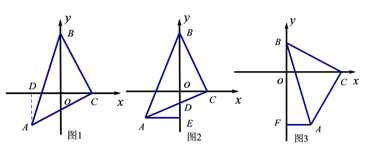
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3 , 则原铁皮的边长为( )
A.10cm
B.13cm
C.14cm
D.16cm -
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上任取一点A,截取AB=20cm,再截取AC=18cm,M、N分别是AB、AC的中点,则M、N两点之间的距离为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式与x2﹣2x+1的和是3x﹣2,则这个多项式为( )
A.x2﹣5x+3
B.﹣x2+x﹣1
C.﹣x2+5x﹣3
D.x2﹣5x﹣13
相关试题

