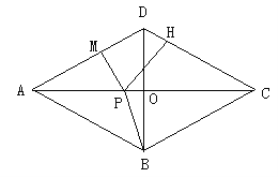
【题目】(13分)如图所示,四边形![]() 中,
中, ![]() 于点
于点![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点。
上的一个动点。
(1)求证: ![]() 。
。
(2)过点![]() 分别作
分别作![]() 于
于![]() 点,作
点,作![]() 于
于![]() 点。
点。
① 试说明![]() 为定值。
为定值。
② 连结![]() ,试探索:在点
,试探索:在点![]() 运动过程中,是否存在点
运动过程中,是否存在点![]() ,使
,使![]() 的值最小。若存在,请求出该最小值;若不存在,请说明理由。
的值最小。若存在,请求出该最小值;若不存在,请说明理由。
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(1)由AC⊥BD,AO=CO,可知BD是AC的垂直平分线,由线段垂直平分线的性质可知AD=DC,AB=BC,同理可得AD=AB,CD=BC,故AB=BC=CD=AD;或先根据对角线互相平分的四边形是平行四边形先证四边形ABCD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形证明四边形ABCD是菱形,进而得出结论;
(2)连接DP,根据题意可知: S△ADC=S△ADP+S△CDP,由三角形的面积公式可知: ![]() ACOD =
ACOD =![]() ADPM+
ADPM+![]() DCPH,将AC、OD、AD、DC的长代入化简即可;
DCPH,将AC、OD、AD、DC的长代入化简即可;
(3))由PM+PH为定值,当PB最短时,PM+PH+PB有最小值,由垂线的性质可知当点P与点O重合时,OB有最小值.
试题解析:
(1)证明:∵AO=CO,BD⊥AC,
∴AD=CD,AB=BC ,
同理可得AD=AB,CD=BC,
∴AB=BC=CD=AD;
另证:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形,
∴AB=BC=CD=AD.
(2)证明:∵AC⊥BD,BO=DO=5,AO=CO=12,
∴由勾股定理得AD=CD=13,
连结DP则S△ADC=S△ADP+S△CDP ,
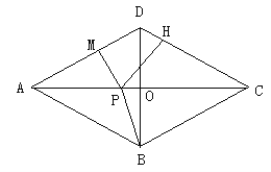
又∵PM⊥AD,PH⊥DC,DO⊥AC,
∴![]()
∴![]()
∴![]() 即
即![]() 为定值;
为定值;
(3)存在点![]() ,使
,使![]() 的值最小.
的值最小.
由(2)可知, ![]() 为定值
为定值
∴要使PM+PH+PB最小,则PB要取最小值
∵BO⊥AC,
∴当P与O重合时,PB最小,最小值为OB=5,
∴PM+PH+PB的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(﹣2a2)4=8a8B.a3+a=a4
C.a5÷a2=a3D.(a+b)2=a2+b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】第五次全国人口普查显示,某市总人口为463万人,用科学记数法表示为( )人.
A.4.63×106
B.4.63×105
C.4.63×102
D.4.63×103 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于四舍五入得到的近似数1.50万,下列说法中正确的是( )
A. 该近似数精确到百分位 B. 该近似数精确到十分位
C. 该近似数精确到千位 D. 该近似数精确到百位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上.
(1)如图1所示,若C的坐标是(2,0),点A的坐标是(﹣2,﹣2),求:点B的坐标;
(思路提示:过点A作AD⊥x轴于点D,通过证明△BOC≌△CDA来达到目的.)
(2)如图2,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴 于E,问BD与AE有怎样的数量关系,并说明理由;
(3)如图3,直角边BC的两个端点在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论①
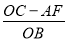 为定值;②
为定值;②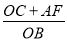 为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.
为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.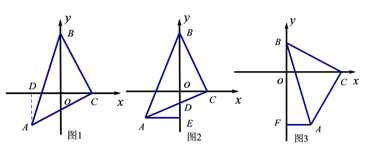
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为射线AB上一点,AB=30,AC比BC的
 多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: ①BC=2AC;②AB=4NQ;③当PB=
多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: ①BC=2AC;②AB=4NQ;③当PB=  BQ时,t=12,其中正确结论的个数是( )
BQ时,t=12,其中正确结论的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3 , 则原铁皮的边长为( )
A.10cm
B.13cm
C.14cm
D.16cm
相关试题

