搜索
【题目】在一条直线上任取一点A，截取AB=20cm，再截取AC=18cm，M、N分别是AB、AC的中点，则M、N两点之间的距离为cm．
参考答案：
【答案】19或1
【解析】解：①当点C在BA延长线上时，如图1， 
∵M是AB中点，N是AC中点，
∴AM= 
AB=10cm，AN= AC=9cm，
∴MN=AM+AN=19cm；
②当点C在线段AB上时，如图2，
∵M是AB中点，N是AC中点，
∴AM= AB=10cm，AN= AC=9cm，
∴MN=AM﹣AN=1cm，
综上，M、N两点之间的距离为19或1cm，
所以答案是：19或1．
【考点精析】本题主要考查了两点间的距离的相关知识点，需要掌握同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C为射线AB上一点，AB=30，AC比BC的
多5，P，Q两点分别从A，B两点同时出发．分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结论： ①BC=2AC；②AB=4NQ；③当PB= 
BQ时，t=12，其中正确结论的个数是（ ）
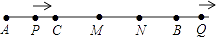
A.0
B.1
C.2
D.3 -
科目： 来源： 题型：
查看答案和解析>>【题目】数据-5，-3，-3，0，1，3的众数是_______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A的坐标是（﹣1，0），点B的坐标是（9，0），以AB为直径作⊙O′，交y轴的负半轴于点C，连接AC、BC，过A、B、C三点作抛物线．
（1）求抛物线的解析式；
（2）点E是AC延长线上一点，∠BCE的平分线CD交⊙O′于点D，连结BD，求直线BD的解析式；
（3）在（2）的条件下，抛物线上是否存在点P，使得∠PDB=∠CBD？如果存在，请求出点P的坐标；如果不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合题。
（1）计算：﹣12016+（﹣5）×[（﹣2）3+2]﹣（﹣4）2÷（﹣
）
（2）解方程：x﹣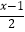
=2﹣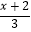 
（3）已知：A= a﹣2（a﹣ 
b2），B=﹣ 
a+ 
b2 ， 且|a+2|+（b﹣3）2=0，求2A﹣6B的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】某海域有A、B、C三艘船正在捕鱼作业，C船突然出现故障，向A、B两船发出紧急求救信号，此时B船位于A船的北偏西72°方向，距A船24海里的海域，C船位于A船的北偏东33°方向，同时又位于B船的北偏东78°方向．
（1）求∠ABC的度数；
（2）A船以每小时30海里的速度前去救援，问多长时间能到出事地点．（结果精确到0.01小时）．
（参考数据：
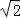≈1.414，
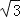≈1.732）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某超市一月份的营业额为10万元，一至三月份的总营业额为45万元，若平均每月的增长率为x，则依题意列方程为（ ）
A. 10（1+x）2＝45B. 10+10×2x＝45
C. 10+10×3x＝45D. 10[1+（1+x）+（1+x）2]＝45
相关试题
