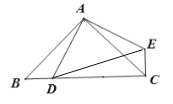
【题目】如图,在△ABC中,∠BAC=90°,AC=AB,点D为BC边上的一个动点(点D不与B,C重合),以AD为边作等腰直角△ADE,∠DAE=90°,连接CE.
(1)求证:△ABD≌△ACE.
(2)试猜想线段BD,CD,DE之间的等量关系,并证明你的猜想.
参考答案:
【答案】(1)见解析;(2)![]() +
+![]() =
=![]()
【解析】
(1)根据SAS,只要证明∠1=∠2即可解决问题;
(2)结论:![]() +
+![]() =
=![]() .证明∠ECD=90°,BD=CE,利用勾股定理即可解决问题.
.证明∠ECD=90°,BD=CE,利用勾股定理即可解决问题.
(1)∵∠DAE=90°,∴∠DAC+∠2=90°.
又∵∠BAC=∠DAC+∠1=90°,∴∠1=∠2.
在△ABD和△ACE中,∵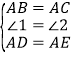 ,∴△ABD≌△ACE.
,∴△ABD≌△ACE.
(2)结论:CD2+BD2=DE2.理由如下:
∵∠BAC=90°,AB=AC,∴∠B=∠3=45°.
由(1)知△ABD≌△ACE,∴∠4=∠B=45°,BD=CE,∴∠ECD=∠3+∠4=90°,∴CD2+CE2=DE2,∴CD2+BD2=DE2.
-
科目: 来源: 题型:
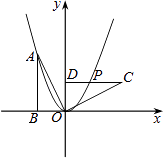
查看答案和解析>>【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
A.(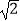 ,
, 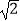 )
)
B.(2,2)
C.(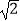 ,2)
,2)
D.(2,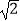 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 ,点
,点 在直线
在直线 上,点
上,点 到直线
到直线 的距离分别为1,2.
的距离分别为1,2.(1)利用直尺和圆规作出以
 为底的等腰△ABC,使点
为底的等腰△ABC,使点 在直线
在直线 上(保留作图痕迹,不写作法).
上(保留作图痕迹,不写作法).(2)若(1)中得到的△ABC为等腰直角三角形,求△ABC的面积.

-
科目: 来源: 题型:
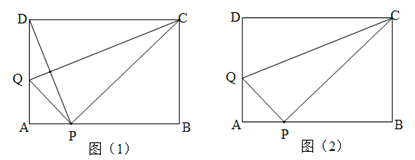
查看答案和解析>>【题目】如图(1)将长方形纸片ABCD的一边CD沿着CQ向下折叠,使点D落在边AB上的点P处.
(1)试判断线段CQ与PD的关系,并说明理由;
(2)如图(2),若AB=CD=5,AD=BC=3.求AQ的长;
(3)如图(2),BC=3,取CQ的中点M,连接MD,PM,若MD⊥PM,求AQ(AB+BC)的值.
-
科目: 来源: 题型:
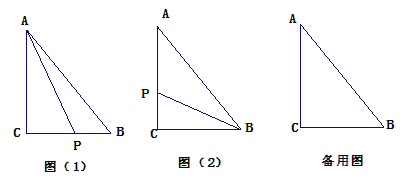
查看答案和解析>>【题目】如图(1)在△ABC中,∠C=90°,AB=25cm,BC=15cm,若动点P从点C开始沿着C→B→A→C的路径运动,且速度为每秒5cm,设点P运动的时间为t秒.
(1)点P运动2秒后,求△ABP的面积;
(2)如图(2),当t为何值时,BP平分∠ABC;
(3)当△BCP为等腰三角形时,直接写出所有满足条件t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ≈1.414.
≈1.414.  ≈1.732)
≈1.732)
相关试题

