【题目】如图,已知直线![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 到直线
到直线![]() 的距离分别为1,2.
的距离分别为1,2.
(1)利用直尺和圆规作出以![]() 为底的等腰△ABC,使点
为底的等腰△ABC,使点![]() 在直线
在直线![]() 上(保留作图痕迹,不写作法).
上(保留作图痕迹,不写作法).
(2)若(1)中得到的△ABC为等腰直角三角形,求△ABC的面积.

参考答案:
【答案】(1)见解析(2)5
【解析】
(1)作出线段BC的垂直平分线交直线a于点A,连结AB,AC,则△ABC即为所求;
(2)过点C作CD⊥a于D,根据同角的余角相等求出∠BAE=∠ACD,然后利用“角角边”证明△ABE≌△CAD,根据全等三角形对应边相等可得AE=CD,BE=AD,再利用勾股定理列式求出AC的长,然后根据等腰直角三角形的性质即可得出结论.
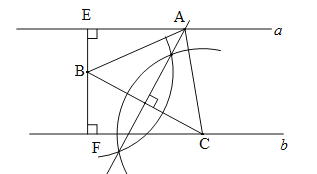
(1)如图所示:△ABC即为所求.
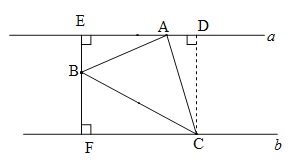
(2)如图,过点C作CD⊥a于D,则∠ACD+∠CAD=90°.
∵△ABC为等腰直角三角形,∴∠BAE+∠CAD=180°﹣90°=90°,∴∠BAE=∠ACD.
在△ABE和△CAD中,∵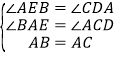 ,∴△ABE≌△CAD(AAS),∴AE=CD,BE=AD.
,∴△ABE≌△CAD(AAS),∴AE=CD,BE=AD.
∵BE=1,BF=2,∴AD=1,AE=CD=1+2=3.在Rt△ACD中,AC=![]() =
=![]() .
.
∵△ABC是等腰直角三角形,∴![]() =5.
=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )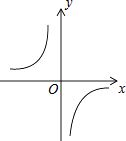
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
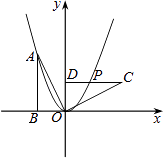
A.(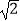 ,
, 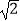 )
)
B.(2,2)
C.(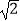 ,2)
,2)
D.(2,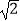 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率. -
科目: 来源: 题型:
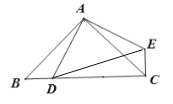
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AC=AB,点D为BC边上的一个动点(点D不与B,C重合),以AD为边作等腰直角△ADE,∠DAE=90°,连接CE.
(1)求证:△ABD≌△ACE.
(2)试猜想线段BD,CD,DE之间的等量关系,并证明你的猜想.
-
科目: 来源: 题型:
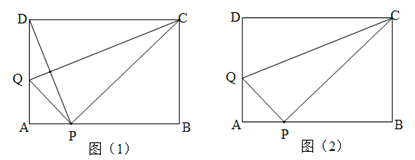
查看答案和解析>>【题目】如图(1)将长方形纸片ABCD的一边CD沿着CQ向下折叠,使点D落在边AB上的点P处.
(1)试判断线段CQ与PD的关系,并说明理由;
(2)如图(2),若AB=CD=5,AD=BC=3.求AQ的长;
(3)如图(2),BC=3,取CQ的中点M,连接MD,PM,若MD⊥PM,求AQ(AB+BC)的值.
-
科目: 来源: 题型:
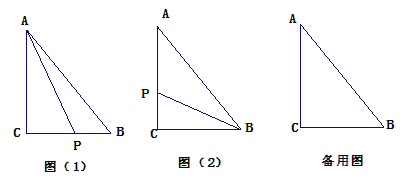
查看答案和解析>>【题目】如图(1)在△ABC中,∠C=90°,AB=25cm,BC=15cm,若动点P从点C开始沿着C→B→A→C的路径运动,且速度为每秒5cm,设点P运动的时间为t秒.
(1)点P运动2秒后,求△ABP的面积;
(2)如图(2),当t为何值时,BP平分∠ABC;
(3)当△BCP为等腰三角形时,直接写出所有满足条件t的值.
相关试题

