【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.
参考答案:
【答案】
(1)
解:两辆汽车所有9种可能的行驶方向如下:
甲汽车 乙汽车 | 左转 | 右转 | 直行 |
左转 | (左转,左转) | (右转,左转) | (直行,左转) |
右转 | (左转,右转) | (右转,右转) | (直行,右转) |
直行 | (左转,直行) | (右转,直行) | (直行,直行) |
(2)
解:由上表知:两辆汽车都向左转的概率是: ![]() .
.
【解析】(1)利用树形图”或“列表法”即可求出两辆汽车行驶方向所有可能的结果;(2)根据(1)中的列表情况即可求出这两辆汽车都向左转的概率.
【考点精析】利用列表法与树状图法对题目进行判断即可得到答案,需要熟知当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
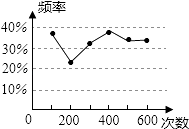
A.掷一枚正六面体的骰子,出现1点的概率
B.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
C.抛一枚硬币,出现正面的概率
D.任意写一个整数,它能被2整除的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )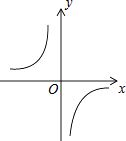
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
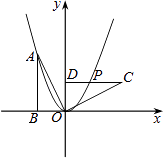
A.(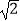 ,
, 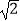 )
)
B.(2,2)
C.(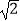 ,2)
,2)
D.(2,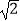 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 ,点
,点 在直线
在直线 上,点
上,点 到直线
到直线 的距离分别为1,2.
的距离分别为1,2.(1)利用直尺和圆规作出以
 为底的等腰△ABC,使点
为底的等腰△ABC,使点 在直线
在直线 上(保留作图痕迹,不写作法).
上(保留作图痕迹,不写作法).(2)若(1)中得到的△ABC为等腰直角三角形,求△ABC的面积.

-
科目: 来源: 题型:
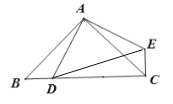
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AC=AB,点D为BC边上的一个动点(点D不与B,C重合),以AD为边作等腰直角△ADE,∠DAE=90°,连接CE.
(1)求证:△ABD≌△ACE.
(2)试猜想线段BD,CD,DE之间的等量关系,并证明你的猜想.
-
科目: 来源: 题型:
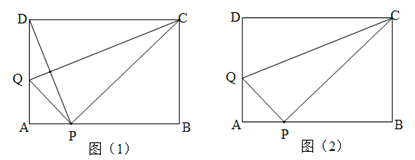
查看答案和解析>>【题目】如图(1)将长方形纸片ABCD的一边CD沿着CQ向下折叠,使点D落在边AB上的点P处.
(1)试判断线段CQ与PD的关系,并说明理由;
(2)如图(2),若AB=CD=5,AD=BC=3.求AQ的长;
(3)如图(2),BC=3,取CQ的中点M,连接MD,PM,若MD⊥PM,求AQ(AB+BC)的值.
相关试题

