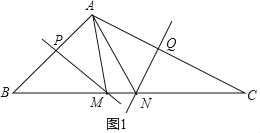
【题目】已知△ABC中,BC=6,AB、AC的垂直平分线分别交边BC于点M、N,若MN=2,则△AMN的周长是_____.
参考答案:
【答案】6或10
【解析】
由直线PM为线段AB的垂直平分线,根据线段垂直平分线定理:线段垂直平分线上的点到线段两端点的距离相等可得AM=BM,同理可得AN=NC,然后表示出三角形AMN的三边之和,等量代换可得其周长等于BC的长,由BC的长即可得到三角形AMN的周长.
如图1,∵直线MP为线段AB的垂直平分线,
∴MA=MB,
又直线NQ为线段AC的垂直平分线,
∴NA=NC,
∴△AMN的周长l=AM+MN+AN=BM+MN+NC=BC,
又BC=6,
则△AMN的周长为6;
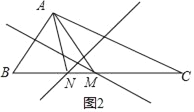
如图2,△AMN的周长l=AM+MN+AN=BM+MN+NC=BC+2MN,
又BC=6,
则△AMN的周长为10,
故答案为:6或10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若一次函数y=ax+b的图象经过二、三、四象限,则二次函数y=ax2+bx的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,
求证:AD平分∠BAC.
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°(___________)
∴∠ADC=∠EGC(等量代换)
∴AD∥EG(_____________)
∴∠1=∠2(___________)
∠E=∠3(___________)
又∵∠E=∠1( 已知)
∴∠2=∠3(___________)
∴AD平分∠BAC(___________).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为_____.

-
科目: 来源: 题型:
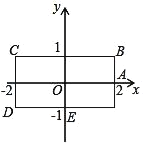
查看答案和解析>>【题目】如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
(1)原理:对于任意两个实数a、b,
若ab>0,则a和b同号,即:
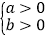 或
或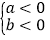 ;
;若ab<0,则a和b异号,即:
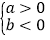 或
或 ;
;(2)对不等式(x+1)(x﹣2)>0来说,把(x+1)和(x﹣2)看成两个数a和b,所以按照上述原理可知:(Ⅰ)
 或(Ⅱ)
或(Ⅱ)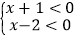 ,所以不等式(x+1)(x﹣2)>0的求解就转化求解不等式组(I)和(Ⅱ).
,所以不等式(x+1)(x﹣2)>0的求解就转化求解不等式组(I)和(Ⅱ).(3)应用:解不等式x2﹣x﹣12>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP= .

相关试题

