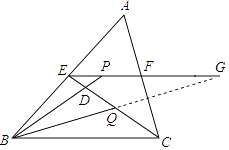
【题目】如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP= . 
参考答案:
【答案】8
【解析】解:如图,延长EF交BQ的延长线于G.
∵EG∥BC,
∴∠G=∠GBC,
∵∠GBC=∠GBP,
∴∠G=∠PBG,
∴PB=PG,
∴PE+PB=PE+PG=EG,
∵3CQ=EC,
∴EQ=2CQ,
∵EG∥BC,
∴ ![]() =
= ![]() =2,∵BC=4,
=2,∵BC=4,
∴EG=8,
∴EP+PB=EG=8,
所以答案是:8.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,BC=6,AB、AC的垂直平分线分别交边BC于点M、N,若MN=2,则△AMN的周长是_____.
-
科目: 来源: 题型:
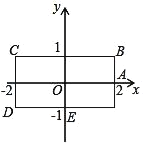
查看答案和解析>>【题目】如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
(1)原理:对于任意两个实数a、b,
若ab>0,则a和b同号,即:
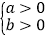 或
或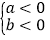 ;
;若ab<0,则a和b异号,即:
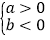 或
或 ;
;(2)对不等式(x+1)(x﹣2)>0来说,把(x+1)和(x﹣2)看成两个数a和b,所以按照上述原理可知:(Ⅰ)
 或(Ⅱ)
或(Ⅱ)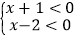 ,所以不等式(x+1)(x﹣2)>0的求解就转化求解不等式组(I)和(Ⅱ).
,所以不等式(x+1)(x﹣2)>0的求解就转化求解不等式组(I)和(Ⅱ).(3)应用:解不等式x2﹣x﹣12>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
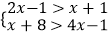 ,并把解集在如图数轴上表示出来.
,并把解集在如图数轴上表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率. -
科目: 来源: 题型:
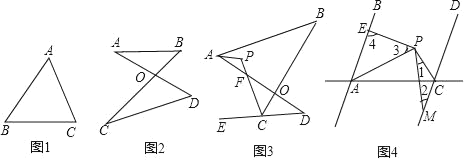
查看答案和解析>>【题目】(1)如图,请证明∠A+∠B+∠C=180°
(2)如图的图形我们把它称为“8字形”,请证明∠A+∠B=∠C+∠D
(3)如图,E在DC的延长线上,AP平分∠BAD,CP平分∠BCE,猜想∠P与∠B、∠D之间的关系,并证明
(4)如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过点P作PM、PE交CD于M,交AB于E,则①∠1+∠2+∠3+∠4不变;②∠3+∠4﹣∠1﹣∠2不变,选择正确的并给予证明.
相关试题

