【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.

(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
参考答案:
【答案】(1)m=2 (2)P(1+![]() ,-9)或P(1-
,-9)或P(1-![]() ,-9)
,-9)
【解析】试题分析:(1)利用待定系数法即可解决问题;
(2)利用方程组首先求出点D坐标.由面积关系,推出点P的纵坐标,再利用待定系数法求出点P的坐标即可.
试题解析:(1)∵抛物线y=-x2+mx+3过(3,0),
∴0=-9+3m+3,
∴m=2
(2)由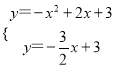 ,得
,得![]() ,
, 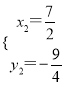 ,
,
∴D(![]() ,-
,-![]() ),
),
∵S△ABP=4S△ABD,
∴![]() AB×|yP|=4×
AB×|yP|=4×![]() AB×
AB×![]() ,
,
∴|yP|=9,yP=±9,
当y=9时,-x2+2x+3=9,无实数解,
当y=-9时,-x2+2x+3=-9,解得:x1=1+![]() ,x2=1-
,x2=1-![]() ,
,
∴P(1+![]() ,-9)或P(1-
,-9)或P(1-![]() ,-9).
,-9).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和等于它的外角和的2倍,那么这个多边形是_____ 边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某NBA职业篮球队15名队员的身高(厘米)依次是: 192、203、205、 188、211、208、207、198、199、 200、203、 205、 196、 212、 205, 这组身高数据中的众数和中位数分别是( )
A.205 203B.212 188C.208 203D.203 198
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD内部作等边三角形BCE,则∠AEB的度数为( )
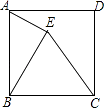
A.60°
B.65°
C.70°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】有一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )
A. △ABC三个角平分线的交点 B. △ABC三边的垂直平分线的交点
C. △ABC三条中线的交点 D. △ABC三条高所在直线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE:∠ECB=3:1,则∠ACE=度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .

相关试题

