【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 . 
参考答案:
【答案】(3,4)或(2,4)或(8,4)
【解析】解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;(2)OD是等腰三角形的一条腰时:①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP= ![]() =
= ![]() =3,则P的坐标是(3,4).②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
=3,则P的坐标是(3,4).②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM= ![]() =3,
=3,
当P在M的左边时,CP=5﹣3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
所以答案是:(3,4)或(2,4)或(8,4).

【考点精析】通过灵活运用等腰三角形的性质和勾股定理的概念,掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-
 x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.
(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )
A. △ABC三个角平分线的交点 B. △ABC三边的垂直平分线的交点
C. △ABC三条中线的交点 D. △ABC三条高所在直线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE:∠ECB=3:1,则∠ACE=度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】地表以下岩层的温度随着所处深度的变化而变化,在这一问题中自变量是( )
A.地表B.岩层的温度C.所处深度D.时间
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分6分)
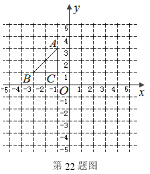
如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(-1,3),B(-3,1),C(-1,1).请解答下列问题:
⑴ 画出△ABC关于y轴对称的△A1B1C1,并写出B1的坐标.
⑵ 画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1,并求出点A1走过的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数y=
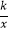 的图象经过点C,一次函数y=ax+b的图象经过点A、C,
的图象经过点C,一次函数y=ax+b的图象经过点A、C, 
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
相关试题

