【题目】设抛物线的解析式为![]() ,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点
,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点![]() (
(![]() ,0 ) (n为正整数 )作x轴的垂线,交抛物线于点
,0 ) (n为正整数 )作x轴的垂线,交抛物线于点![]() ,连接
,连接![]() ,得直角三角形
,得直角三角形![]() .
.
(1)求a的值;
(2)直接写出线段![]() ,
,![]() 的长(用含n的式子表示);
的长(用含n的式子表示);
(3)在系列Rt△![]() 中,探究下列问题:
中,探究下列问题:
①当n为何值时,Rt△![]() 是等腰直角三角形?
是等腰直角三角形?
②设1≤k<m≤n (k,m均为正整数),问是否存在Rt△![]() 与Rt△
与Rt△![]() 相似?若存在,求出其相似比;若不存在,说明理由.
相似?若存在,求出其相似比;若不存在,说明理由.
参考答案:
【答案】(1)2;(2)![]() =
=![]() ,
,![]() =
=![]() ;(3)①3;②相似比是8:1或64:1.
;(3)①3;②相似比是8:1或64:1.
【解析】
试题分析:(1)把A(1,2)代入![]() ,即可得出结论;
,即可得出结论;
(2)根据题意直接写出![]() ,
,![]() 即可;
即可;
(3) ① 若Rt△![]() 是等腰直角三角形,则
是等腰直角三角形,则![]() =
=![]() ,则
,则![]() ,解方程即可得到n的值;
,解方程即可得到n的值;
②若Rt△![]() 与Rt△
与Rt△![]() 相似,则
相似,则![]() 或
或![]() ,解得k+m=6.由m>k,且k,m均为正整数,得到
,解得k+m=6.由m>k,且k,m均为正整数,得到![]() 或
或![]() ,即可得到相似比.
,即可得到相似比.
试题解析:(1)把A(1,2)代入![]() ,得:
,得:![]() ,∴a=2;
,∴a=2;
(2)![]() =
=![]() ,
,![]() =
=![]() =
=![]() ;
;
(3) ① 若Rt△![]() 是等腰直角三角形,则
是等腰直角三角形,则![]() =
=![]() ,则
,则![]() ,解得:n=3;
,解得:n=3;
②若Rt△![]() 与Rt△
与Rt△![]() 相似,则
相似,则![]() 或
或![]() ,∴
,∴![]() 或
或![]() ,∴m=k(舍去),或k+m=6.∵m>k,且k,m均为正整数,∴
,∴m=k(舍去),或k+m=6.∵m>k,且k,m均为正整数,∴![]() 或
或![]() ,∴相似比=
,∴相似比=![]() =
=![]() =8:1,或
=8:1,或![]() =
=![]() =64:1. ∴相似比是8:1或64:1.
=64:1. ∴相似比是8:1或64:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN;

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,是一元一次方程的是( )
A.2x+5y=6 B.3x﹣2 C.x2=1 D.3x+5=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣12x+18= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:

(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
-
科目: 来源: 题型:
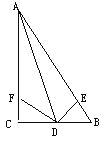
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,上海市全社会用于环境保护的资金约为90 800 000 000元,这个数用科学记数法表示为( ).
A.908×108B.90.8×109C.9.08×1011D.9.08×1010.
相关试题

