【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN;

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。

参考答案:
【答案】(1)见解析;(2)MN=BN-AM
【解析】
试题分析:(1)根据同角的余角相等可得∠MAC=∠NCB,又∠AMC=∠CNB=90°,AC=BC,即可证得△AMC≌△CNB,从而可得AM=CN,MC=BN,即可得到结论;
(2)类似于(1)的方法,证得△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系.
∵∠C=90°
∴∠MCA+∠BCN=90°
∵AM⊥MN,BN⊥MN
∴∠AMC=∠CNB=90°
∴∠MAC+∠MCA=90°
∴∠MAC=∠BCN
在△AMC和△CNB中
∠MAC=∠BCN
∠AMC=∠CMB,
AC=BC
∴△AMC≌△CNB
∴AM=CN,MC=BN
∴MN=MC+CN=AM+BN
(2)(7分)答: MN=BN-AM
证明:∵∠AMC=∠BNC=90°,
∴∠ACM+∠NCB=90°,
∠NCB+∠CBN=90°,
故∠ACM=∠CBN,
在△AMC和△CNB中,
∠ACM=∠CBN
∠AMC=∠BNC=90°
AC=BC,
∴△AMC≌△CNB,
∴CM =BN,
CN=AM,
∴MN=CM-CN=BN-AM,
∴MN=BN-AM。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E
(1)试说明:BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果;
(3)若直线AE绕A点旋转到图(3)位置时(BD>CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果,不需说明理由.

-
科目: 来源: 题型:
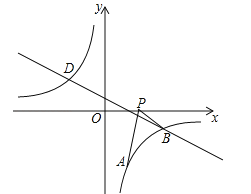
查看答案和解析>>【题目】如图,已知点A(1,a)是反比例函数
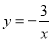 的图象上一点,直线
的图象上一点,直线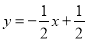 与反比例函数
与反比例函数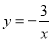 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )
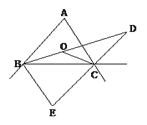
A. 15° B. 20° C. 25° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,是一元一次方程的是( )
A.2x+5y=6 B.3x﹣2 C.x2=1 D.3x+5=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣12x+18= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线的解析式为
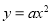 ,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点
,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点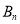 (
( ,0 ) (n为正整数 )作x轴的垂线,交抛物线于点
,0 ) (n为正整数 )作x轴的垂线,交抛物线于点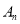 ,连接
,连接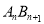 ,得直角三角形
,得直角三角形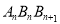 .
.(1)求a的值;
(2)直接写出线段
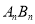 ,
,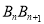 的长(用含n的式子表示);
的长(用含n的式子表示);(3)在系列Rt△
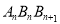 中,探究下列问题:
中,探究下列问题:①当n为何值时,Rt△
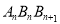 是等腰直角三角形?
是等腰直角三角形?②设1≤k<m≤n (k,m均为正整数),问是否存在Rt△
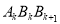 与Rt△
与Rt△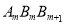 相似?若存在,求出其相似比;若不存在,说明理由.
相似?若存在,求出其相似比;若不存在,说明理由.
相关试题

