【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):
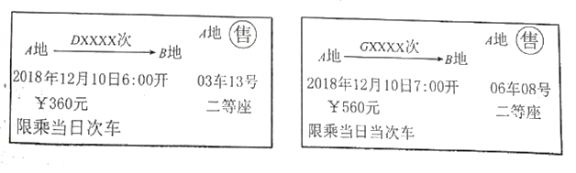
![]() 根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
![]() 已知该动车和高铁的平均速度分别为
已知该动车和高铁的平均速度分别为![]() ,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2
,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2![]() .求
.求![]() 两地之间的距离.
两地之间的距离.
参考答案:
【答案】(1)同;(2)![]() 两地之间的距离是
两地之间的距离是![]() .
.
【解析】
(1)根据相向而行和同向而行的定义即可得出答案;
(2)先设出A、B两地之间的距离,再根据“高铁比动车早到2h”列出方程,解方程即可得出答案.
解:(1)∵动车和高铁的起始点和目的地均相同
∴动车和高铁是同向而行.
(2)设A、B两地之问的距离为xkm,
根据题意得:![]() ,
,
解得:![]() .
.
答:A、B两地之间的距离是1200km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年假期某校对操场进行了维修改造,如图是操场的一角.在长为
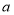 米,宽为
米,宽为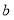 米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为
米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为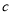 米.
米.(1)直接写出一个篮球场的长和宽;(用含字母
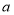 ,
,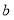 ,
,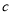 的代数式表示)
的代数式表示)(2)用含字母
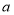 ,
,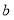 ,
,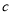 的代数式表示这两个篮球场占地面积的和,并求出当
的代数式表示这两个篮球场占地面积的和,并求出当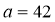 ,
,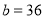 ,
, 时,这两个篮球场占地面积的和.
时,这两个篮球场占地面积的和.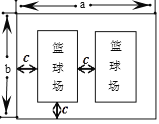
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年2月,市城区公交车施行全程免费乘坐政策,标志着我市公共交通建设迈进了一个新的时代.下图为某一条东西方向直线上的公交线路,东起职教园区站,西至富士康站,途中共设
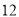 个上下车站点,如图所示:
个上下车站点,如图所示: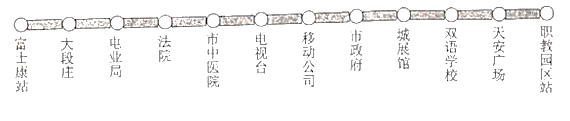
某天,小王从电业局站出发,始终在该线路的公交站点做志愿者服务,到
 站下车时,本次志愿者服务活动结束,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站):
站下车时,本次志愿者服务活动结束,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站): 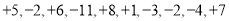 ;
;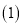 请通过计算说明
请通过计算说明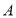 站是哪一站?
站是哪一站? 若相邻两站之间的平均距离为
若相邻两站之间的平均距离为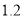 千米,求这次小王志愿服务期间乘坐公交车行进的总路程是多少千米?
千米,求这次小王志愿服务期间乘坐公交车行进的总路程是多少千米? -
科目: 来源: 题型:
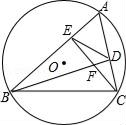
查看答案和解析>>【题目】如图,⊙O的半径为2,弦BC=2
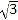 ,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:
,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:①∠A始终为60°;
②当∠ABC=45°时,AE=EF;
③当△ABC为锐角三角形时,ED=
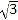 ;
;④线段ED的垂直平分线必平分弦BC.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实验课程改革,初三年级设罝了A,B,C,D四门不同的拓展性课程(每位学生只选修其中一门,所有学生都有一门选修课程),学校摸底调査了初三学生的选课意向,并将调查结果绘制成两个不完整的统计图,问该校初三年级共有多少学生?其中要选修B、C课程的各有多少学生?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+bx+c(b,c都是常数)的图象经过点(1,0)和(0,2).
(1)当﹣2≤x≤2时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m+n=1,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=
 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=
 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
相关试题

