【题目】小明解方程![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
参考答案:
【答案】(1)一,方程两边都乘以(或都除以)同一个不为0的数,方程的解不变;(2)见解析.
【解析】
(1)根据等式的基本性质判断可得;
(2)根据解分式方程的步骤依次计算可得.
(1)一 方程两边都乘以(或都除以)同一个不为0的数,方程的解不变
(2)解答过程如下:
方程两边都乘以![]() ,得
,得 ![]() .
.
解得 ![]() .
.
检验,当![]() 时
时![]()
所以 ![]() 是原方程的解.
是原方程的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的表达式为:y=-3x+3,且直线l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,求点P的坐标.

-
科目: 来源: 题型:
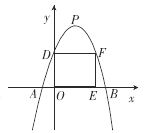
查看答案和解析>>【题目】已知抛物线y=-x2+bx+c的顶点P的坐标为(n,n2+2n+1)(n≥1).
(1)求b与n,c与n之间的关系式;
(2)若抛物线y=-x2+bx+c与x轴交于点A,B(点A在点B的左边),点P到AB的距离等于线段AB长的2倍,求此抛物线y=-x2+bx+c的解析式;
(3)设抛物线y=-x2+bx+c与y轴交于点D,O为原点,矩形OEFD的顶点E,F分别在x轴和该抛物线上,当矩形OEFD的面积为20时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌
 ,△AEB≌
,△AEB≌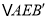 ,且
,且 ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105°B.100°C.110°D.115°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ABCD和
ABCD和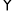 AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将
AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将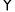 ABCD固定不动,
ABCD固定不动,  AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当
AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当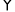 AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C. 
探究一:
(1)在图2的情形下,求旋转角α的度数;
探究二:
(2)如图3,当
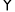 AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;探究三:
(3)如图1,连接CF,BF,在旋转过程中△BCF的面积是否存在最大的情形,如果存在,求出最大面积,如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,

(1)如图1,
①线段CD和BE的数量关系是 ;
②请写出线段AD,BE,DE之间的数量关系并证明.
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名采购员同去一家饲料公司购买两次饲料.两次饲料的价格分别为
 元/千克和
元/千克和 元/千克(
元/千克( 、
、 都为正数,且
都为正数,且 ),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.
),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.(1)用含
 、
、 的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?
的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?(2)若规定:谁两次购买饲料的平均单价低,谁的购货方式合算,请你判断甲、乙两名采购员购货方式哪个更合算?说明理由.
相关试题

