【题目】如图,直线l1的表达式为:y=-3x+3,且直线l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,求点P的坐标.

参考答案:
【答案】(1)(1,0);(2)![]() ;(3)
;(3)![]() ;(4)(6,3).
;(4)(6,3).
【解析】
(1)由题意已知l1的解析式,令y=0求出x的值即可;
(2)根据题意设l2的解析式为y=kx+b,并由题意联立方程组求出k,b的值;
(3)由题意联立方程组,求出交点C的坐标,继而即可求出S△ADC;
(4)由题意根据△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到AD的距离进行分析计算.
解:(1)由y=-3x+3,令y=0,得-3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,y=![]() ,代入表达式y=kx+b,
,代入表达式y=kx+b,
∴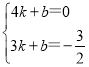 ,
,
∴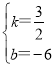 ,
,
∴直线l2的解析表达式为![]() ;
;
(3)由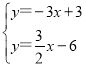 ,解得
,解得![]() ,
,
∴C(2,-3),
∵AD=3,
∴![]() ;
;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|-3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x-6,y=3,
∴1.5x-6=3,解得x=6,
所以P(6,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】张新是某县城中学的在校住宿生,开学初父母通过估算为他预存了一个学期的伙食费1600元,学校的学生食堂规定一天的伙食标准:早餐每人4元,中餐、晚餐只能各选一份价格如下表中的饭菜.
(1)请问该校每位住宿生一天的伙食费有几种可能的价格?其金额各是多少元?
(2)若张新选择(1)中一天的伙食费的两种价格,并计划用膳110天,且刚好用完预存款,那么他应有哪几种选择价格的方案?每种方案中两种价格各用膳多少天?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水 3000 吨,计划内用水每吨收费 0.5元,超计划部分每吨按 0.8 元收费.
(1)写出该单位水费 y(元)与每月用水量 x(吨)之间的函数关系式:(写出自变量取值范围)
①用水量小于等于 3000 吨 ;
②用水量大于 3000 吨 .
(2)某月该单位用水 3200 吨,水费是 元;若用水 2800 吨,水费 元.
(3)若某月该单位缴纳水费 1580 元,则该单位用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组乘汽车从
 地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:
地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位: ):
):-4,+7,-9,+8,+6,-4,-3.
(1)收工时汽车共行驶了多少千米?
(2)收工时,汽车距
 地多远?
地多远? (3)在检修时,第几个检修点离
 地最远,最远距离是多少?
地最远,最远距离是多少? -
科目: 来源: 题型:
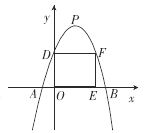
查看答案和解析>>【题目】已知抛物线y=-x2+bx+c的顶点P的坐标为(n,n2+2n+1)(n≥1).
(1)求b与n,c与n之间的关系式;
(2)若抛物线y=-x2+bx+c与x轴交于点A,B(点A在点B的左边),点P到AB的距离等于线段AB长的2倍,求此抛物线y=-x2+bx+c的解析式;
(3)设抛物线y=-x2+bx+c与y轴交于点D,O为原点,矩形OEFD的顶点E,F分别在x轴和该抛物线上,当矩形OEFD的面积为20时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌
 ,△AEB≌
,△AEB≌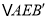 ,且
,且 ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105°B.100°C.110°D.115°
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明解方程
 =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
相关试题

