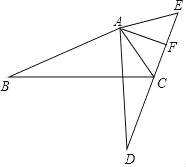
【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
参考答案:
【答案】(1)证明见解析;(2)40°
【解析】
(1)由∠BAD=∠CAE可证得∠BAC=∠DAE,结合已知条件利用SAS证明△ABC≌△ADE; (2)根据三角形的内角和定理求得∠ACB=50°,利用全等三角形的性质可得∠ACB=∠AED=50°,由等腰三角形三线合一的性质可得AF⊥CE,即可求得∠FAE的度数.
(1)∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
∵AB=AD,AC=AE,
∴△ABC≌△ADE(SAS);
(2)∵∠B+∠ACB+∠BAC=180°,
∴∠ACB=180°-∠B-∠BAC=50°,
∵△ABC≌△ADE,
∴∠ACB=∠AED=50°,
∵点F是CE的中点,
∴AF⊥CE,
∴∠FAE=90°-∠E=40° .
-
科目: 来源: 题型:
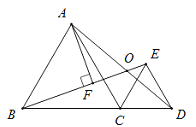
查看答案和解析>>【题目】如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
A. 1 B.
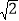 C.
C. 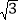 D. 2
D. 2 -
科目: 来源: 题型:
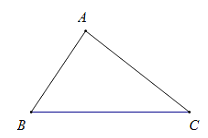
查看答案和解析>>【题目】如图,已知△ABC,按下列要求作图(第(1)、(2)小题用尺规作图,第(3)小题不限作图工具,保留作图痕迹).
(1)作∠B的角平分线;
(2)作BC的中垂线;
(3)以BC边所在直线为对称轴,作△ABC的轴对称图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.

请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BA=BC,BE平分∠ABC,CD⊥BD,且CD=BD.
(1)求证:BF=AC;
(2)若AD=
 ,求CF的长.
,求CF的长.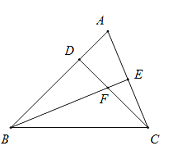
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣4|﹣22+
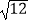 ﹣tan60°(说明:本题不允许使用计算器计算)
﹣tan60°(说明:本题不允许使用计算器计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
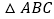 和
和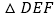 是两个全等的三角形,
是两个全等的三角形,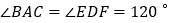 ,
,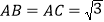 .现将
.现将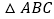 和
和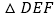 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,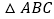 保持不动,
保持不动,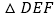 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在
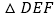 的运动过程中,
的运动过程中,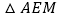 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.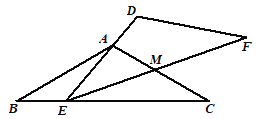
相关试题

