【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°) 
(1)当OC∥AB时,旋转角α=度;
(2)线段AC与BD有何数量关系,请仅就图2给出证明. 
(3)当A、C、D三点共线时,求BD的长.
(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
参考答案:
【答案】
(1)60或240
(2)解:结论:AC=BD,理由如下:
如图2中,
∵∠COD=∠AOB=60°,
∴∠COA=∠DOB,
在△AOC和△BOD中,
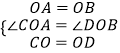 ,
,
∴△AOC≌△BOD,
∴AC=BD
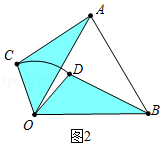
(3)解:①如图3中,当A、C、D共线时,作OH⊥AC于H.
在Rt△COH中,∵OC=1,∠COH=30°,
∴CH=HD= ![]() ,OH=
,OH= ![]() ,
,
在Rt△AOH中,
AH= ![]() =
= ![]() ,
,
∴BD=AC=CH+AH= ![]() .
.
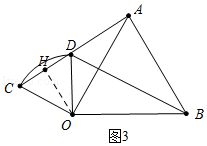
如图4中,当A、C、D共线时,作OH⊥AC于H.
易知AC=BD=AH﹣CH= ![]() ,
,
综上所述,当A、C、D三点共线时,BD的长为 ![]() 或
或 ![]()
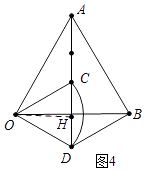
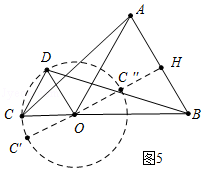
(4)解:如图5中,由题意,点C在以O为圆心,1为半径的⊙O上运动,过点O作OH⊥AB于H,直线OH交⊙O于C′、C″,线段CB的长即为PC的最大值,线段C″H的长即为PC的最小值.易知PC的最大值=3,PC的最小值= ![]() ﹣1.
﹣1.
【解析】解:(1)如图1中, 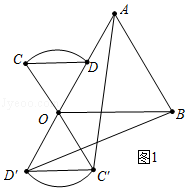
∵△ABC是等边三角形,
∴∠AOB=∠COD=60°,
∴当点D在线段AD和线段AD的延长线上时,OC∥AB,
此时旋转角α=60°或240°.
所以答案是60或240;
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答问题
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为:x+3=2,解得x=﹣1
当x+3<0时,原方程可化为:x+3=﹣2,解得x=﹣5
所以原方程的解是x=﹣1,x=﹣5
(1)解方程:|3x﹣2|﹣4=0;
(2)探究:当b为何值时,方程|x﹣2|=b ①无解;②只有一个解;③有两个解.
(3)
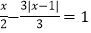
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(根)
40
30
24
20
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:(每小题5分,共30分)
(1)

(2)

(3)

(4)

(5)解方程:

(6)解方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
 的最小整数解为方程
的最小整数解为方程 的解,求代数式
的解,求代数式 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】红星中学九年级(1)班三位教师决定带领本班
 名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。
名学生利用假期去某地旅游,枫江旅行社的收费标准为:教师全价,学生半价;而东方旅行社不管教师还是学生一律八折优惠,这两家旅行社的全价都是500元。(1)用含
 的式子表示三位教师和
的式子表示三位教师和 位学生参加这两家旅行社所需的费用各是多少元;
位学生参加这两家旅行社所需的费用各是多少元;(2)如果
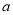 =50时,请你计算选择哪一家旅行社较为合算?
=50时,请你计算选择哪一家旅行社较为合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式ax5+bx3+3x+c,当x=0时,该代数式的值为﹣1.
(1)求c的值;
(2)已知当x=3时,该式子的值为9,试求当x=﹣3时该式子的值;
(3)在第(2)小题的已知条件下,若有3a=5b成立,试比较a+b与c的大小?
相关试题

