【题目】先阅读下列解题过程,然后解答问题
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为:x+3=2,解得x=﹣1
当x+3<0时,原方程可化为:x+3=﹣2,解得x=﹣5
所以原方程的解是x=﹣1,x=﹣5
(1)解方程:|3x﹣2|﹣4=0;
(2)探究:当b为何值时,方程|x﹣2|=b ①无解;②只有一个解;③有两个解.
(3)![]()
参考答案:
【答案】(1)方程无解;(2)①无解,b<﹣1;②只有一个解,b=﹣1;③有两个解,b>﹣1.
【解析】
(1)首先要认真审题,解此题时要理解绝对值的意义,要会去绝对值号,然后化为一元一次方程即可求得.
(2)运用分类讨论进行解答.
解:(1)|3x﹣2|+x=0; 当x≥0时,此方程不成立;
当x<0时,原方程化为﹣3x+2+x=0,解得:x=1,不合题意,
所以此方程无解
(2)|x﹣2|=b+1 ①无解b+1<0,b<﹣1;②只有一个解b+1=0,b=﹣1;③有两个解b+1>0,b>﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写字时一项主要基本功,也是素质教育的重要部分,为了了解我校学生的书写情况,随机对部分学生进行测试,测试结果分为四个等级:优秀、良好、合格、不合格;根据调查结果绘制了下列两幅不完整的统计图,请你根据统计图提供的信息,回答以下问题:
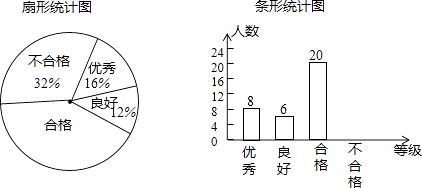
(1)扇形统计图中,“合格”的百分比为;
(2)本次抽测不合格等级学生有人;
(3)随机抽取了5名等级为“优秀”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,求刚好抽到同性别学生的概率;
(4)若该校共有2000名学生,估计该校书写“不合格”等级学生约有多少人? -
科目: 来源: 题型:
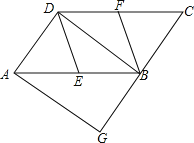
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列等式:①由a=b,得5﹣2a=5﹣2b;②由a=b,得ac=bc;③由a=b,得
 ;④由
;④由 ,得3a=2b;
,得3a=2b;⑤由a2=b2,得a=b.其中正确的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(根)
40
30
24
20
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:(每小题5分,共30分)
(1)

(2)

(3)

(4)

(5)解方程:

(6)解方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△AOB中,将扇形COD按图1摆放,使扇形的半径OC、OD分别与OA、OB重合,OA=OB=2,OC=OD=1,固定等边△AOB不动,让扇形COD绕点O逆时针旋转,线段AC、BD也随之变化,设旋转角为α.(0<α≤360°)

(1)当OC∥AB时,旋转角α=度;
(2)线段AC与BD有何数量关系,请仅就图2给出证明.
(3)当A、C、D三点共线时,求BD的长.
(4)P是线段AB上任意一点,在扇形COD的旋转过程中,请直接写出线段PC的最大值与最小值.
相关试题

