【题目】如图，点O为Rt△ABC斜边AB上一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD．
（1）求证：AD平分∠BAC；
（2）若∠BAC=60°，OA=2，求阴影部分的面积（结果保留π）．

参考答案：

【答案】
（1）证明：∵⊙O切BC于D，

∴OD⊥BC，

∵AC⊥BC，

∴AC∥OD，

∴∠CAD=∠ADO，

∵OA=OD，

∴∠OAD=∠ADO，

∴∠OAD=∠CAD，

即AD平分∠CAB


（2）设EO与AD交于点M，连接ED．

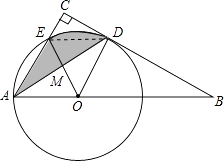
∵∠BAC=60°，OA=OE，

∴△AEO是等边三角形，

∴AE=OA，∠AOE=60°，

∴AE=AO=OD，

又由（1）知，AC∥OD即AE∥OD，

∴四边形AEDO是菱形，则△AEM≌△DMO，∠EOD=60°，

∴S△AEM=S△DMO，

∴S阴影=S扇形EOD= = ．


【解析】（1）由Rt△ABC中，∠C=90°，⊙O切BC于D，易证得AC∥OD，继而证得AD平分∠CAB．（2）如图，连接ED，根据（1）中AC∥OD和菱形的判定与性质得到四边形AEDO是菱形，则△AEM≌△DMO，则图中阴影部分的面积=扇形EOD的面积．
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径，以及对扇形面积计算公式的理解，了解在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．

关闭