Question

【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）、B（3，0）．

（1）求b、c的值；
（2）如图1直线y=kx+1（k＞0）与抛物线第一象限的部分交于D点，交y轴于F点，交线段BC于E点．求 的最大值；
（3）如图2，抛物线的对称轴与抛物线交于点P、与直线BC相交于点M，连接PB．问在直线BC下方的抛物线上是否存在点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：将点A（﹣1，0）、B（3，0）带入到抛物线解析式中得：

，

解得：

（2）

解：作DN∥CF交CB于N，如图1所示．

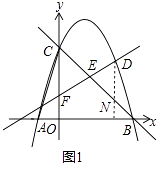
∵DN∥CF，

∴△DEN∽△FEC，

∴ ．

∵抛物线的解析式为y=﹣x2+2x+3，

∴点C的坐标为（0，3）．

∴直线BC的解析式为y=﹣x+3．

令直线y=kx+1中x=0，则y=1，

即点F的坐标为（0，1）．

设点D的坐标为（m，﹣m2+2m+3），则点N的坐标为（m，﹣m+3），

∴DN=﹣m2+3m，CF=3﹣1=2，

∴ = ，

∵DN=﹣m2+3m=﹣ + 的最大值为 ，

∴ 的最大值为

（3）

解：假设存在符合题意的点Q．

∵抛物线的解析式为y=﹣x2+2x+3=﹣（x﹣1）2+4，

∴P点的坐标为（1，4），PM的解析式为x=1，

∵直线BC的解析式为y=﹣x+3，

∴M的坐标为（1，2），

∵点G的坐标为（1，0），

∴PM=GM=2．

设PM与x轴交于点G，过点G作作直线BC的平行线，如图2所示．

∴过点G与BC平行的直线为y=﹣x+1．

联立直线与抛物线解析式得： ，

解得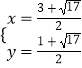： 或 ．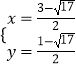

∴点Q的坐标为（ ，﹣ ）或（ ，﹣ ）．

∵平行线间距离处处相等，且点M为线段PG的中点，

∴点Q到直线BC的距离与点P到直线的距离相等．

故在直线BC下方的抛物线上存在点Q，使得△QMB与△PMB的面积相等，点Q的坐标为（ ，﹣ ）或（ ，﹣ ）

【解析】（1）将点A、B的坐标带入到抛物线解析式中，得出关于b、c的二元一次方程组，解方程组即可得出结论；（2）作DN∥CF交CB于N，由DN∥CF可得出△DEN∽△FEC，根据相似三角形的性质得出 ，由（1）可得出抛物线的解析式，令抛物线解析式中x=0则可得出点C的坐标，由点B、C的坐标可得出直线BC的解析式，设出点D的坐标，则可得出点N的坐标，由直线DF的解析式可得出点F的坐标，从而得出DN、CF的长度，由DN的长度结合二次函数的性质即可得出结论；（3）假设存在符合题意的点Q．设PM与x轴交于点G，过点G作作直线BC的平行线．由抛物线的解析式可得出顶点P的坐标，由此得出对称轴的解析式，结合直线BC的解析式可得出点M的坐标，结合点G的坐标可知PM=GM，由此得出满足题意的点Q为“过点G与直线BC平行的直线和抛物线的交点”，由G点的坐标结合直线BC的解析式即可得出过点G与BC平行的直线的解析式，联立直线与抛物线解析式得出关于x、y的二元二次方程组，解方程即可得出结论．
【考点精析】认真审题，首先需要了解一元二次方程的定义(只有一个未知数，并且未知数的项的最高系数为2的方程为一元二次方程)，还要掌握抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．)的相关知识才是答题的关键．