【题目】如图,△ABC的边BC上的高为AF,AC边上的高为BG,中线为AD.已知AF=6,BC=10,BG=5.
(1)求△ABC的面积;
(2)求AC的长;
(3)试说明△ABD和△ACD的面积相等.

参考答案:
【答案】(1)30;(2)12;(3)见解析.
【解析】
(1)直接利用三角形的面积计算方法计算得出答案即可;(2)利用三角形的面积计算公式建立方程求得答案即可;(3)利用三角形的面积计算公式以及两个三角形底和高的关系得出答案即可.
(1)∵△ABC的边BC上的高为AF,AF=6,BC=10,
∴△ABC的面积为![]() BC·AF=
BC·AF=![]() ×10×6=30.
×10×6=30.
(2)∵AC边上的高为BG,BG=5,
∴△ABC的面积为![]() AC·BG=30,即
AC·BG=30,即![]() AC×5=30,∴AC=12.
AC×5=30,∴AC=12.
(3)∵△ABC的中线为AD,
∴BD=CD.
∵△ABD以BD为底,△ACD以CD为底,而且等高,
∴S△ABD=S△ACD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些相同的“○”按如图所示的规律依次摆放,观察每个“稻草人”中的“○”的个数,则第20个“稻草人”中有个“○”.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠1=∠2,G为AD边上的中点,延长BG交AC于点E,且满足BE⊥AC;F为AB上一点,CF⊥AD于点H.下列判断:①线段AG是△ABE的角平分线;②BE是△ABD边AD上的中线;③线段AE是△ABG的边BG上的高;④∠1+∠FBC+∠FCB=90°.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B(3,0).

(1)求b、c的值;
(2)如图1直线y=kx+1(k>0)与抛物线第一象限的部分交于D点,交y轴于F点,交线段BC于E点.求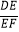 的最大值;
的最大值;
(3)如图2,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.问在直线BC下方的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=500,∠C=600,求∠DAE和∠BOA的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.

(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
相关试题

