【题目】如图，AE是半圆O的直径，弦AB=BC=4 ，弦CD=DE=4，连结OB，OD，则图中两个阴影部分的面积和为 ．

参考答案：

【答案】10π
【解析】解：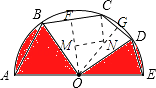
∵弦AB=BC，弦CD=DE，
∴点B是弧AC的中点，点D是弧CE的中点，
∴∠BOD=90°，
过点O作OF⊥BC于点F，OG⊥CD于点G．
则BF=FC=2 ，CG=GD=2，∠FOG=45°，
在四边形OFCG中，∠FCD=135°，
过点C作CN∥OF，交OG于点N，
则∠FCN=90°，∠NCG=135°﹣90°=45°，
∴△CNG为等腰三角形，
∴CG=NG=2，
过点N作NM⊥OF于点M，则MN=FC=2 ，
在等腰三角形MNO中，NO= MN=4，
∴OG=ON+NG=6，
在Rt△OGD中，OD= = =2 ，
即圆O的半径为2 ，
故S阴影=S扇形OBD= =10π．
所以答案是：10π．
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握垂径定理(垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧)的相关知识才是答题的关键．

关闭