Question

【题目】如图，△ABC是等边三角形，点D是BC边上一动点，点E，F分别在AB，AC边上，连接AD，DE，DF，且∠ADE=∠ADF=60°．

小明通过观察、实验，提出猜想：在点D运动的过程中，始终有AE=AF，小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

想法1：利用AD是∠EDF的角平分线，构造△ADF的全等三角形，然后通过等腰三角形的相关知识获证．

想法2：利用AD是∠EDF的角平分线，构造角平分线的性质定理的基本图形，然后通过全等三角形的相关知识获证．

想法3：将△ACD绕点A顺时针旋转至△ABG，使得AC和AB重合，然后通过全等三角形的相关知识获证．

请你参考上面的想法，帮助小明证明AE=AF．（一种方法即可）

Answer 1

【答案】见解析

【解析】

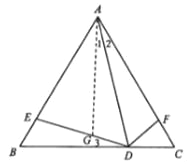
想法1：在DE上截取DG=DF，连接AG，先判定△ADG≌△ADF，得到AG=AF，再根据∠AEG=∠AGE，得出AE=AG，进而得到AE=AF；

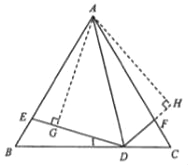
想法2：过A作AG⊥DE于G，AH⊥DF于H，依据角平分线的性质得到AG=AH，进而判定△AEG≌△AFH，即可得到AE=AF；

想法3：将△ACD绕着点A顺时针旋转至△ABG，使得AC与AB重合，连接DG，判定△AGD是等边三角形，进而得出△AGE≌△ADF，即可得到AE=AF．

证明：

想法1：如图，在DE上截取DG=DF，连接AG，

∵△ABC是等边三角形，

∴∠B=∠C=60°，

∵∠ADE=∠ADF=60°，AD=AD，

∴△ADG≌△ADF，

∴AG=AF，∠1=∠2，

∵∠ADB=60°+∠3=60°+∠2，

∴∠3=∠2，

∴∠3=∠1，

∵∠AEG=60°+∠3，∠AGE=60°+∠1，

∴∠AEG=∠AGE，

∴AE=AG，

∴AE=AF；

想法2：如图，过A作AG⊥DE于G，AH⊥DF于H，

∵∠ADE=∠ADF=60°，

∴AG=AH，

∵∠FDC=60°﹣∠1，

∴∠AFH=∠DFC=60°+∠1，

∵∠AED=60°+∠1，

∴∠AEG=∠AFH，

∴△AEG≌△AFH，

∴AE=AF；

想法3：如图，将△ACD绕着点A顺时针旋转至△ABG，使得AC与AB重合，连接DG，

∴△ABG≌△ACD，

∴AG=AD，∠GAB=∠DAC，

∵△ABC是等边三角形，

∴∠BAC=∠ABC=∠C=60°，

∴∠GAD=60°，

∴△AGD是等边三角形，

∴∠ADG=∠AGD=60°，

∵∠ADE=60°，

∴G，E，D三点共线，

∴△AGE≌△ADF，

∴AE=AF．