【题目】如图，等腰直角三角形ABC顶点A在x轴上，∠BCA=90°，AC=BC=2 ，反比例函数y= （x＞0）的图象分别与AB，BC交于点D，E．连结DE，当△BDE∽△BCA时，点E的坐标为 ．

参考答案：

【答案】（ ， ）
【解析】解：如图1，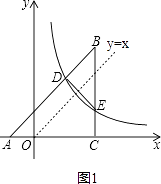
∵点D、E是反比例函数y= （x＞0）的图象上的点，
∴设点D的坐标是（m， ），点E的坐标是（n， ），
又∵∠BCA=90°，AC=BC=2 ，
∴C（n，0），B（n，2 ），A（n﹣2 ，0），
设直线AB的解析式是：y=ax+b，
则
解得
∴直线AB的解析式是：y=x+2 ﹣n．
又∵△BDE∽△BCA，
∴∠BDE=∠BCA=90°，
∴直线y=x与直线DE垂直，
∴点D、E关于直线y=x对称，
∴ = ，
∴mn=3，或m+n=0（舍去），
又∵点D在直线AB上，
∴ =m+2 ﹣n，mn=3，
整理，可得
2n2﹣2 n﹣3=0，
解得n= 或n=﹣ （舍去），
∴点E的坐标是（ ， ）．
所以答案是：（ ， ）．
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点，需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．

关闭