【题目】如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°. 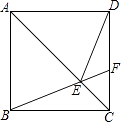
(1)∠ACB的大小=(度);
(2)求证:△ABE≌△ADE;
(3)∠AED的大小=(度).
参考答案:
【答案】
(1)45
(2)证明:∵四边形ABCD是正方形,
∴AB=AD,∠EAB=∠EAD,
在△EAB和△EAD中,
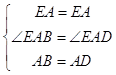 ,
,
∴△EAB≌△EAD.
(3)65
【解析】(1)解:∵四边形ABCD是正方形, ∴∠BCD=90°,∠ACB= ![]() BCD=
BCD= ![]() ×90°=45°.
×90°=45°.
所以答案是45.
(3.)解:∵△EAB≌△EAD,
∴∠AED=∠AEB,
∵∠AEB=∠EBC+∠BCE=20°+45°=65°.
∴∠AED=65°.
所以答案是65.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在ABCD中,E是AD边的中点,连接BE.
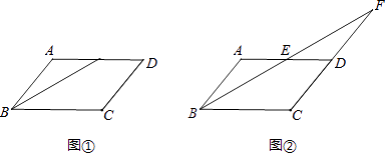
(1)如图①,若BC=2,则AE的长=;
(2)如图②,延长BE交CD的延长线于点F,求证:FD=AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三条边距离相等的点是( )
A. 三条高线的交点 B. 三条中线的交点
C. 三个内角平分线的交点 D. 三边垂直平分线的交点
-
科目: 来源: 题型:
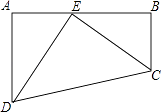
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠B=90°,AB=25,AD=15,BC=10,点E是AB上一点,且DE=CE,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式2(a2﹣2ab﹣b2)﹣(a2+mab+2b2)不含ab项,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点的位置如图所示,将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
利用网格点画图: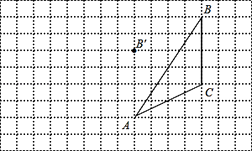
(1)画出△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x+3)2与|y﹣2|互为相反数,z是绝对值最小的有理数,求(x+y)y+xyz的值.
相关试题

