【题目】如图,四边形ABCD中,∠A=∠B=90°,AB=25,AD=15,BC=10,点E是AB上一点,且DE=CE,求AE的长. 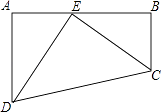
参考答案:
【答案】解:设AE=x, ∵AB=25,
∴BE=25﹣x,
∵∠A=∠B=90°,
∴DE2=AD2+AE2=152+x2 ,
CE2=BC2+BE2=102+(25﹣x)2 ,
∵DE=CE,
∴152+x2=102+(25﹣x)2 ,
解得x=10,
所以,AE=10.
【解析】设AE=x,表示出BE=25﹣x,再分别利用勾股定理列式表示出DE2、CE2 , 然后根据DE=CE列方程求解即可.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF= .
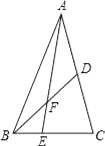
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在ABCD中,E是AD边的中点,连接BE.
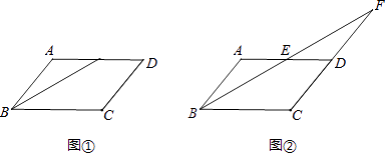
(1)如图①,若BC=2,则AE的长=;
(2)如图②,延长BE交CD的延长线于点F,求证:FD=AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三条边距离相等的点是( )
A. 三条高线的交点 B. 三条中线的交点
C. 三个内角平分线的交点 D. 三边垂直平分线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°.
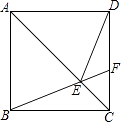
(1)∠ACB的大小=(度);
(2)求证:△ABE≌△ADE;
(3)∠AED的大小=(度). -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式2(a2﹣2ab﹣b2)﹣(a2+mab+2b2)不含ab项,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点的位置如图所示,将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
利用网格点画图: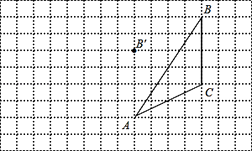
(1)画出△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 .
相关试题

