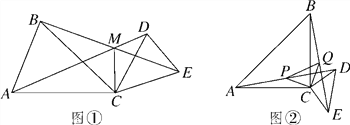
【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
参考答案:
【答案】(1)证明见解析;(2)∠AMB=α;(3)△CPQ为等腰直角三角形,证明见解析.
【解析】试题分析:(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CAD=∠CBE,再根据∠AFC=∠BFH,即可得到∠AMB=∠ACB=α;
(3)先根据SAS判定△ACP≌△BCQ,再根据全等三角形的性质,得出CP=CQ,∠ACP=∠BCQ,最后根据∠ACB=90°即可得到∠PCQ=90°,进而得到△PCQ为等腰直角三角形.
试题解析:(1)证明:如图①,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE.在△ACD和△BCE中,
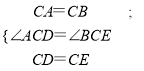
∴△ACD≌△BCE(SAS),
∴BE=AD.
(2)解:如图①,∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠BAC+∠ABC=180°-α,
∴∠BAM+∠ABM=180°-α,
∴∠AMB=180°-(180°-α)=α.
(3)解:△CPQ为等腰直角三角形.
证明:如图②,由(1)可得,BE=AD.
∵AD,BE的中点分别为点P,Q,
∴AP=BQ.
∵△ACD≌△BCE,
∴∠CAP=∠CBQ.在△ACP和△BCQ中,
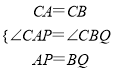
∴△ACP≌△BCQ(SAS),
∴CP=CQ且∠ACP=∠BCQ.
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台,和液晶显示器8台,共需要资金7000元,若购进电脑机箱两台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元,根据市场行情,销售电脑机箱,液晶显示器一台分别可获得10元和160元,改经销商希望销售完这两种商品,所获得利润不少于4100元,试问:该经销商有几种进货方案?哪种方案获利最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=
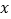 ,BC=
,BC=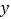 ,且
,且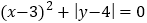 .
.(1)求AD和BC的长;
(2)你认为AD和BC还有什么关系?并验证你的结论;
(3)取AB中点F,连接EF,且EF∥AD∥BC。若EF=
 ,你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.
,你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.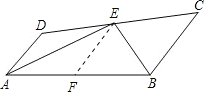
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(3m+2)(3m﹣2)﹣(2m+3)(2m﹣2),其中m=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3292a+1÷27a+1=81,求a的值.
相关试题

