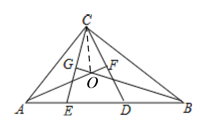
【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.

参考答案:
【答案】见解析
【解析】试题分析:
(1)由AF垂直平分CD可得AC=AD,再由等腰三角形的“三线合一”可得∠FAB=![]() ∠CAB,同理可得∠GBA=
∠CAB,同理可得∠GBA=![]() ∠CBA;如图,设AF、BG相交于点O,则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-
∠CBA;如图,设AF、BG相交于点O,则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-![]() (180°-∠ACB)=135°,由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
(180°-∠ACB)=135°,由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
(2)思路同(1)只需把∠ACB=90°换成∠ACB= ![]() 可解得∠DCE=90°-
可解得∠DCE=90°- ![]() .
.
试题解析:
(1)如图,设AF、BG相交于点O,连接CO,
∵AF垂直平分CD,
∴AC=AD,∠CFO=90°,∴∠FAB=![]() ∠CAB.
∠CAB.
同理可得:∠CGO=90°,∠GBA=![]() ∠CBA.
∠CBA.
∴∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-![]() (180°-∠ACB)=90°+
(180°-∠ACB)=90°+![]() ∠ACB=135°,
∠ACB=135°,
∵四边形GOFC的内角和为360°,
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-135°
=45°.
(2)同(1)可得∠GOF=90°+![]() ∠ACB=90°+
∠ACB=90°+ ![]() ,∠CFO=90°,∠CGO=90°,
,∠CFO=90°,∠CGO=90°,
∵四边形GOFC的内角和为360°,
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-(90°+ ![]() )
)
=90°- ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.

-
科目: 来源: 题型:
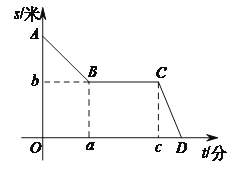
查看答案和解析>>【题目】李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.
(1)求a,b,c的值;
(2)求李老师从学校到家的总时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台,和液晶显示器8台,共需要资金7000元,若购进电脑机箱两台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元,根据市场行情,销售电脑机箱,液晶显示器一台分别可获得10元和160元,改经销商希望销售完这两种商品,所获得利润不少于4100元,试问:该经销商有几种进货方案?哪种方案获利最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
-
科目: 来源: 题型:
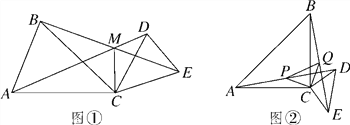
查看答案和解析>>【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=
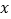 ,BC=
,BC=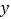 ,且
,且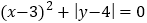 .
.(1)求AD和BC的长;
(2)你认为AD和BC还有什么关系?并验证你的结论;
(3)取AB中点F,连接EF,且EF∥AD∥BC。若EF=
 ,你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.
,你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.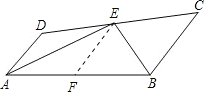
相关试题

