【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
参考答案:
【答案】C
【解析】分析:根据AD=AB和三角形内角和、外角性质,寻找∠C和∠BAC的关系的表达式;再根据BE=BC,寻找∠C和∠BAC关系的另一种表达式,由此可得关于∠BAC的方程,求得的度数,代入即可求得∠C.
详解:
∵AD=AB,
∴∠ADB=![]() (180°﹣
(180°﹣![]() ∠BAC)=90°﹣
∠BAC)=90°﹣![]() ∠BAC,
∠BAC,
∴∠C=∠ADB﹣∠DAC=![]() (180°﹣
(180°﹣![]() ∠BAC)=90°﹣
∠BAC)=90°﹣![]() ∠BAC﹣
∠BAC﹣![]() ∠BAC=90°﹣
∠BAC=90°﹣![]() ∠BAC;
∠BAC;
∵BE=BC,
∴∠C=∠BEC=∠BAC+∠ABE=∠BAC+![]() (180°﹣
(180°﹣![]() ∠BAC)=∠BAC+45°﹣
∠BAC)=∠BAC+45°﹣![]() ∠BAC=45°+
∠BAC=45°+![]() ∠BAC,
∠BAC,
∴90°﹣![]() ∠BAC=45°+
∠BAC=45°+![]() ∠BAC,
∠BAC,
解得∠BAC=![]() ,
,
∴∠C=90°﹣![]() .
.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为
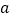 的正方形的边长增加
的正方形的边长增加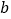 ,得到一个边长为
,得到一个边长为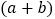 的正方形.在图1的基础上,某同学设计了一个解释验证
的正方形.在图1的基础上,某同学设计了一个解释验证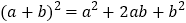 的方案(详见方案1)
的方案(详见方案1)
方案1.如图2,用两种不同的方式表示边长为
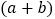 的正方形的面积.
的正方形的面积.方式1:
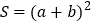
方式2:
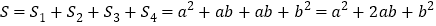
因此,
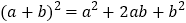
(1)请模仿方案1,在图1的基础上再设计一种方案,用以解释验证
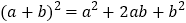 ;
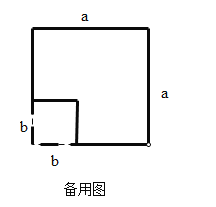
;(2)如图3,在边长为
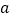 的正方形纸片上剪掉边长为
的正方形纸片上剪掉边长为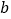 的正方形,请在此基础上再设计一个方案用以解释验证
的正方形,请在此基础上再设计一个方案用以解释验证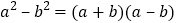 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如右图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y3<y2;其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 1个
-
科目: 来源: 题型:
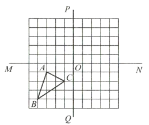
查看答案和解析>>【题目】如图,在正方形网格当中,三角形
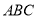 的三个顶点都在格点上.直线
的三个顶点都在格点上.直线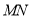 与直线
与直线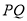 相交于点
相交于点 .
.
(1)画出将三角形
 向右平移5个单位长度后的三角形
向右平移5个单位长度后的三角形 (点
(点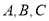 的对应点分别是点
的对应点分别是点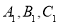 ).
).(2)画出三角形
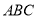 关于直线
关于直线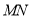 对称的三角形
对称的三角形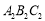 (点
(点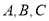 的对应点分别是点
的对应点分别是点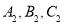 ).
).(3)画出将三角形
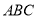 绕着点
绕着点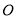 旋转
旋转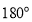 后的三角形
后的三角形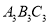 (点
(点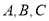 的对应点分别是点
的对应点分别是点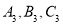 ).
).(4)在三角形
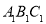 ,
,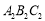 ,
,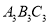 中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称
中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称 -
科目: 来源: 题型:
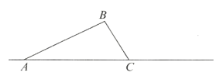
查看答案和解析>>【题目】如图,在三角形
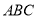 中,
中,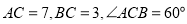 .将三角形
.将三角形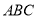 绕着点
绕着点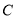 旋转,使得点
旋转,使得点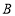 落在直线
落在直线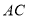 上的点
上的点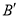 ,点
,点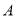 落在点
落在点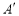 .
.
(1)画出旋转后的三角形
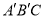 .
.(2)求线段
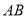 在旋转的过程中所扫过的面积(保留
在旋转的过程中所扫过的面积(保留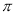 ).
).(3)如果在三角形
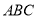 中,
中,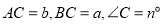 (其中
(其中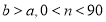 ).其他条件不变,请你用含有
).其他条件不变,请你用含有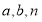 的代数式,直接写出线段
的代数式,直接写出线段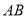 旋转的过程中所扫过的面积(保留
旋转的过程中所扫过的面积(保留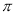 ).
). -
科目: 来源: 题型:
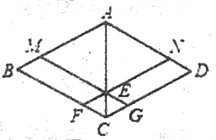
查看答案和解析>>【题目】已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E;
(1)如图,求证:四边形AMEN是菱形;
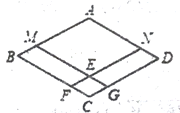
(2)如图,连接AC,在不添加任何辅助线的情况下,请直接写出面积相等的四边形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M;
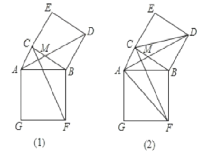
(1)求证:△ABD≌△FBC;
(2) 如图(2),已知AD=6,求四边形AFDC的面积;
相关试题

